Word2vec
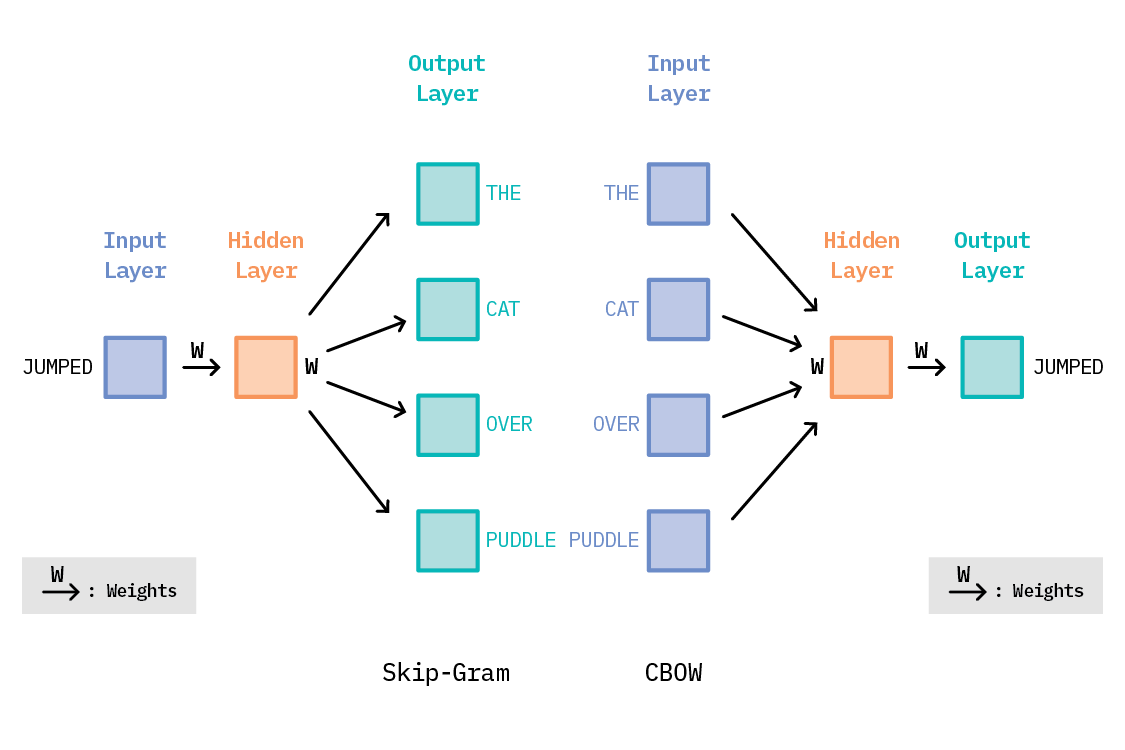
Word2vec uses the co-occurrence of words in a sentence to learn embeddings for each word that capture the semantic meaning of that word. At its core, word2vec is a simple, shallow neural network, with a single hidden layer. In its skip-gram version, it takes as input a word, and tries to predict the context of words around it as the output. For instance, consider this sentence:
“The cat jumped over the puddle.”
Given the central word “jumped,” the model will be able to predict the surrounding words: “The,” “cat,” “over,” “the,” “puddle.”
Another approach—Continuous Bag of Words (CBOW)—treats the words “The,” “cat,” “over,” “the,” and “puddle” as the context, and predicts the center word: “jumped.”
CBOW and Skip-Gram
There are two models for Word2Vec: Continous Bag Of Words (CBOW) and Skip-Gram. While Skip-Gram model predicts context words given a center word, CBOW model predicts a center word given context words. According to Mikolov:
Skip-gram: works well with small amount of the training data, represents well even rare words or phrases
CBOW: several times faster to train than the skip-gram, slightly better accuracy for the frequent words
Skip-Gram model is a better choice most of the time due to its ability to predict infrequent words, but this comes at the price of increased computational cost. If training time is a big concern, and you have large enough data to overcome the issue of predicting infrequent words, CBOW model may be a more viable choice. The details of CBOW model won't be covered in this post.
Skip-gram model
Skip-Gram model seeks to optimize the word weight (embedding) matrix by correctly predicting context words, given a center word. In the other words, the model wants to maximize the probability of correctly predicting all context words at the same time, given a center word. Maximizing the probability of predicting context words leads to optimizing the weight matrix (θ) that best represents words in a vector space. Mathematically, it can be expressed as: