LESSR

research paper

Tianwen Chen and Raymond Chi-Wing Wong, “LESSR: Handling Information Loss of Graph Neural Networks for Session-based Recommendation”. KDD, 2020.

Recently, graph neural networks (GNNs) have gained increasing popularity due to their convincing performance in various applications. Many previous studies also attempted to apply GNNs to session-based recommendation and obtained promising results. However, we spot that there are two information loss problems in these GNN-based methods for session-based recommendation, namely the lossy session encoding problem and the ineffective long-range dependency capturing problem. The first problem is the lossy session encoding problem. Some sequential information about item transitions is ignored because of the lossy encoding from sessions to graphs and the permutation-invariant aggregation during message passing. The second problem is the ineffective long-range dependency capturing problem. Some long-range dependencies within sessions cannot be captured due to the limited number of layers. To solve the first problem, we propose a lossless encoding scheme and an edge-order preserving aggregation layer based on GRU that is dedicatedly designed to process the losslessly encoded graphs. To solve the second problem, we propose a shortcut graph attention layer that effectively captures long-range dependencies by propagating information along shortcut connections. By combining the two kinds of layers, we are able to build a model that does not have the information loss problems and outperforms the state-of-the-art models on three public datasets.

Architecture

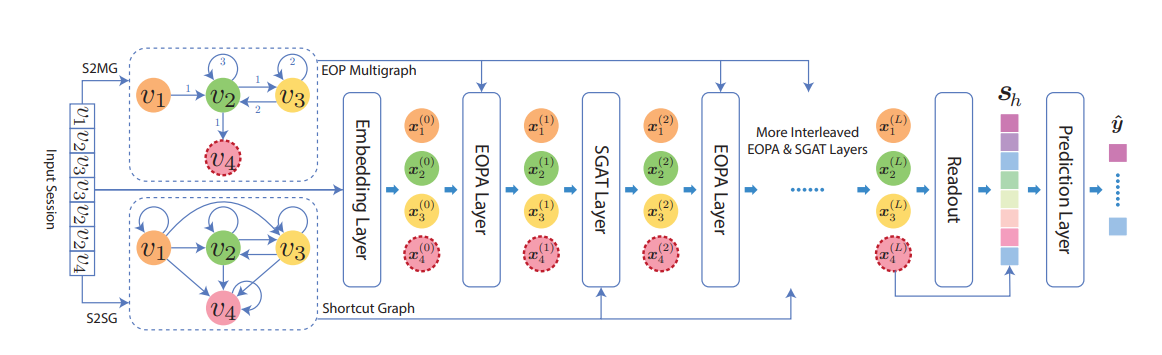
The overview of the proposed model LESSR. Given a session, an edge-order preserving (EOP) multigraph and a shortcut graph is computed. The initial node representations $x_i^{(0)}$ are the item embeddings. The graphs and the node representations are passed as input to multiple interleaved EOPA and SGAT layers. Each layer outputs the new node representations. The readout layer computes a graph-level representation, which is combined with the recent interests to form the session embedding $s_ℎ$. Finally, the prediction layer computes the probability distribution of the next item $\hat{y}$.

A given input session is first converted to a losslessly encoded graph called edge-order preserving (EOP) multigraph and a shortcut graph where the EOP multigraph could address the lossy session encoding problem and the shortcut graph could address the ineffective long-range dependency capturing problem. Then, the graphs along with the item embeddings are passed to multiple edge-order preserving aggregation (EOPA) and shortcut graph attention (SGAT) layers to generate latent features of all nodes. The EOPA layers capture local context information using the EOP multigraph and the SGAT layers effectively capture long-range dependencies using the shortcut graph. Then, a readout function with attention is applied to generate a graph-level embedding from all node embeddings. Finally, we combine the graph-level embedding with users’ recent interests to make recommendations.

Converting Sessions to Graphs

To process sessions using a GNN, sessions must be converted to graphs first. LESSR uses S2MG that converts sessions to EOP multigraphs, and then another method called S2SG that converts sessions to shortcut graphs.

In the literature of session-based recommendation, there are two common methods to convert sessions into graphs.

The first method, S2G, converts a session to an unweighted directed graph $G=(V,E)$ where the node set $V$ consists of the unique items in the session, and the edge set $E$ contains an edge ($u,v$) if $u=s_{i,t}$, and $v=s_{i,t+1}$ for some $1 \leq t < l_i$.

In the second method, S2WG, the edges of the converted graph are weighted, where the weight of an edge ($u,v$) is the number of times that the transition $u → v$ appears in the session.

To address the lossy conversion issue, LESSR uses S2MG (session to EOP multigraph) which converts a session to a directed multigraph that preserves the edge order. For each transition u → v in the original session, we create an edge (u, v). The graph is a multigraph because if there are multiple transitions from u to v, we will create multiple edges from u to v. Then, for each node v, the edges in $E_{in}(v)$ can be ordered by the time of their occurrences in the session. We record the order by giving each edge in $E_{in}(v)$ an integer attribute which indicates its relative order among the edges in $E_{in}(v)$. The edge occurs first in $E_{in}(v)$ is given 1, the next edge in $E_{in}(v)$ is given 2 and so on.

The weighted graph (a), EOP multigraph (b) and shortcut graph (c) of session [$v_1, v_2, v_3, v_3, v_2, v_2, v_4$] converted by S2WG, S2MG and S2SG, respectively. Note that the weights in (a) are omitted because they are all 1.

To handle the ineffective long-range dependency problem in existing GNN-based models for session-based recommendation, LESSR uses the shortcut graph attention (SGAT) layer. The SGAT layer requires an input graph that is different from the above EOP multigraph. The input graph is converted from the input session using the following method called S2SG (session to shortcut graph).

Links

• https://www.kdd.org/kdd2020/accepted-papers/view/handling-information-loss-of-graph-neural-networks-for-session-based-recomm
• https://github.com/twchen/lessr
• https://dl.acm.org/doi/pdf/10.1145/3394486.3403170