LightGCN

GCN is a representative model of graph neural networks that applies message passing to aggregate neighborhood information. The message passing layer with self-loops is defined as follows:

E^{(l+1)} = \sigma(\hat{D}^{-1/2} \hat{A}\hat{D}^{-1/2}E^{(l)}W^{(l)})

where,

$\hat{A} = A + I$ , and $\hat{D} = D + I$
$𝐴$ , $𝐷$ , $𝐼$ are the adjacency matrix, the diagonal node degree matrix, and the identity matrix, respectively
$𝐼$ is used to integrate self-loop connections on nodes
$𝐸^{(𝑙)}$ and $W^{(𝑙)}$ denote the representation matrix and the weight matrix for the $𝑙$ -th layer
$\sigma(·)$ is a non-linear activation function (e.g., ReLU).

LightGCN is the simplified GCN model that removes feature transformations (i.e., $𝑊^{(𝑙)}$ ) and non-linear activations (i.e., 𝜎). Its message passing layer can thus be expressed as follows:

E^{(l+1)} = (\hat{D}^{-1/2} \hat{A}\hat{D}^{-1/2}E^{(l)})

Given self-loop connections, we can rewrite the message passing operations for user 𝑢 and item 𝑖 as follows:

e_u^{(l+1)} = \dfrac{1}{d_u + 1} e_u^{(l)} + \sum_{k \in \mathcal{N}(u)} \dfrac{1}{\sqrt{d_u+1}\sqrt{d_k+1}} e_k^{(l)}

e_i^{(l+1)} = \dfrac{1}{d_i + 1} e_i^{(l)} + \sum_{v \in \mathcal{N}(i)} \dfrac{1}{\sqrt{d_i+1}\sqrt{d_i+1}} e_v^{(l)}

where,

𝑢 and 𝑣 denote users while 𝑖 and 𝑘 denote items
$e_u^{(l)}$ and $e_i^{(l)}$ denote the embeddings of user 𝑢 and item 𝑖 at layer 𝑙
$\mathcal{N}(𝑢)$ and $\mathcal{N}(𝑖)$ represent their neighbor node sets, respectively
$𝑑_𝑢$ denotes the original degree of the node 𝑢.

LightGCN takes the dot product of the two embedding as the final logit to capture the preference of user 𝑢 on item 𝑖. Thus we obtain:

e_u^{(l+1)} \cdot e_i^{(l+1)} = \alpha_{ui}(e_u^{(l)} \cdot e_i^{(l)}) + \sum_{k \in \mathcal{N}(u)}\alpha_{ik}(e_i^{(l)} \cdot e_k^{(l)}) + \sum_{v \in \mathcal{N}(i)}\alpha_{uv}(e_u^{(l)} \cdot e_v^{(l)}) + \sum_{k \in \mathcal{N}(u)}\sum_{v \in \mathcal{N}(i)}\alpha_{kv}(e_k^{(l)} \cdot e_v^{(l)})

Therefore, we can observe that multiple different types of collaborative signals, including user-item relationships (𝑢-𝑖 and 𝑘-𝑣), item-item relationships (𝑘-𝑖), and user-user relationships (𝑢-𝑣), are captured when training GCN-based models with message passing layers. This also reveals why GCN-based models are effective for CF.

LightGCN-single, a variant of LightGCN are also proposed in the paper, where only the k-th embeddings, $e_u^{(k)}$ , $e_i^{(k)}$ , are used as final embeddings. This variant, instead of the original LightGCN, is used here for its better performance and is named sLightGCN for short.

research paper

Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, Yongdong Zhang, and Meng Wang, “LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation”. SIGIR, 2020.

Graph Convolution Network (GCN) has become new state-of-the-art for collaborative filtering. Nevertheless, the reasons of its effectiveness for recommendation are not well understood. Existing work that adapts GCN to recommendation lacks thorough ablation analyses on GCN, which is originally designed for graph classification tasks and equipped with many neural network operations. However, we empirically find that the two most common designs in GCNs -- feature transformation and nonlinear activation -- contribute little to the performance of collaborative filtering. Even worse, including them adds to the difficulty of training and degrades recommendation performance.

In this work, we aim to simplify the design of GCN to make it more concise and appropriate for recommendation. We propose a new model named LightGCN, including only the most essential component in GCN -- neighborhood aggregation -- for collaborative filtering. Specifically, LightGCN learns user and item embeddings by linearly propagating them on the user-item interaction graph, and uses the weighted sum of the embeddings learned at all layers as the final embedding. Such simple, linear, and neat model is much easier to implement and train, exhibiting substantial improvements (about 16.0\% relative improvement on average) over Neural Graph Collaborative Filtering (NGCF) -- a state-of-the-art GCN-based recommender model -- under exactly the same experimental setting. Further analyses are provided towards the rationality of the simple LightGCN from both analytical and empirical perspectives.

Architecture

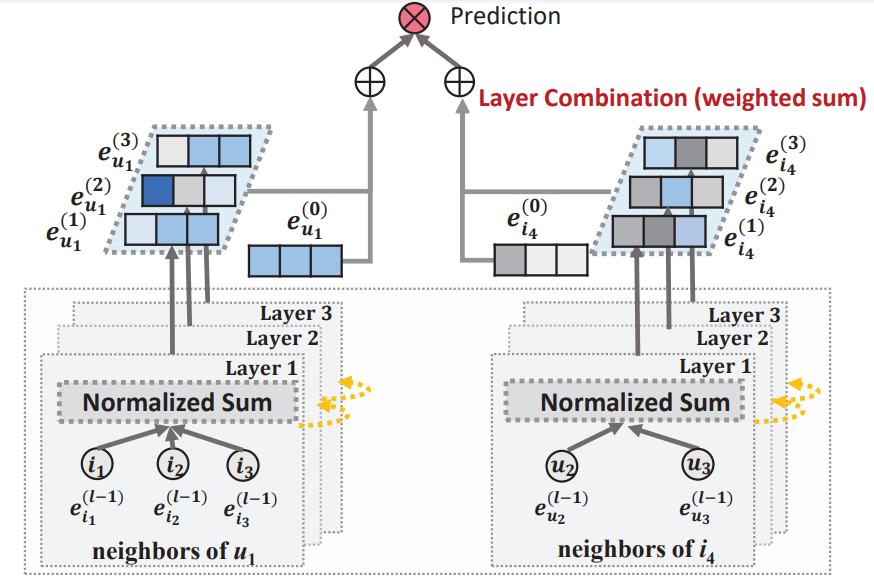
/img/content-models-raw-mp2-lightgcn-untitled.png

Implementation

PyTorch Implementation

'''
Created on October 1, 2020

@author: Tinglin Huang (huangtinglin@outlook.com)
'''
import torch
import torch.nn as nn

class GraphConv(nn.Module):
    """
    Graph Convolutional Network
    """
    def __init__(self, n_hops, n_users, interact_mat,
                 edge_dropout_rate=0.5, mess_dropout_rate=0.1):
        super(GraphConv, self).__init__()

        self.interact_mat = interact_mat
        self.n_users = n_users
        self.n_hops = n_hops
        self.edge_dropout_rate = edge_dropout_rate
        self.mess_dropout_rate = mess_dropout_rate

        self.dropout = nn.Dropout(p=mess_dropout_rate)  # mess dropout

    def _sparse_dropout(self, x, rate=0.5):
        noise_shape = x._nnz()

        random_tensor = rate
        random_tensor += torch.rand(noise_shape).to(x.device)
        dropout_mask = torch.floor(random_tensor).type(torch.bool)
        i = x._indices()
        v = x._values()

        i = i[:, dropout_mask]
        v = v[dropout_mask]

        out = torch.sparse.FloatTensor(i, v, x.shape).to(x.device)
        return out * (1. / (1 - rate))

    def forward(self, user_embed, item_embed,
                mess_dropout=True, edge_dropout=True):
        # user_embed: [n_users, channel]
        # item_embed: [n_items, channel]

        # all_embed: [n_users+n_items, channel]
        all_embed = torch.cat([user_embed, item_embed], dim=0)
        agg_embed = all_embed
        embs = [all_embed]

        for hop in range(self.n_hops):
            interact_mat = self._sparse_dropout(self.interact_mat,
                                                self.edge_dropout_rate) if edge_dropout \
                                                                        else self.interact_mat

            agg_embed = torch.sparse.mm(interact_mat, agg_embed)
            if mess_dropout:
                agg_embed = self.dropout(agg_embed)
            # agg_embed = F.normalize(agg_embed)
            embs.append(agg_embed)
        embs = torch.stack(embs, dim=1)  # [n_entity, n_hops+1, emb_size]
        return embs[:self.n_users, :], embs[self.n_users:, :]

class LightGCN(nn.Module):
    def __init__(self, data_config, args_config, adj_mat):
        super(LightGCN, self).__init__()

        self.n_users = data_config['n_users']
        self.n_items = data_config['n_items']
        self.adj_mat = adj_mat

        self.decay = args_config.l2
        self.emb_size = args_config.dim
        self.context_hops = args_config.context_hops
        self.mess_dropout = args_config.mess_dropout
        self.mess_dropout_rate = args_config.mess_dropout_rate
        self.edge_dropout = args_config.edge_dropout
        self.edge_dropout_rate = args_config.edge_dropout_rate
        self.pool = args_config.pool
        self.n_negs = args_config.n_negs
        self.ns = args_config.ns
        self.K = args_config.K

        self.device = torch.device("cuda:0") if args_config.cuda else torch.device("cpu")

        self._init_weight()
        self.user_embed = nn.Parameter(self.user_embed)
        self.item_embed = nn.Parameter(self.item_embed)

        self.gcn = self._init_model()

    def _init_weight(self):
        initializer = nn.init.xavier_uniform_
        self.user_embed = initializer(torch.empty(self.n_users, self.emb_size))
        self.item_embed = initializer(torch.empty(self.n_items, self.emb_size))

        # [n_users+n_items, n_users+n_items]
        self.sparse_norm_adj = self._convert_sp_mat_to_sp_tensor(self.adj_mat).to(self.device)

    def _init_model(self):
        return GraphConv(n_hops=self.context_hops,
                         n_users=self.n_users,
                         interact_mat=self.sparse_norm_adj,
                         edge_dropout_rate=self.edge_dropout_rate,
                         mess_dropout_rate=self.mess_dropout_rate)

    def _convert_sp_mat_to_sp_tensor(self, X):
        coo = X.tocoo()
        i = torch.LongTensor([coo.row, coo.col])
        v = torch.from_numpy(coo.data).float()
        return torch.sparse.FloatTensor(i, v, coo.shape)

    def forward(self, batch=None):
        user = batch['users']
        pos_item = batch['pos_items']
        neg_item = batch['neg_items']  # [batch_size, n_negs * K]

        # user_gcn_emb: [n_users, channel]
        # item_gcn_emb: [n_users, channel]
        user_gcn_emb, item_gcn_emb = self.gcn(self.user_embed,
                                              self.item_embed,
                                              edge_dropout=self.edge_dropout,
                                              mess_dropout=self.mess_dropout)

        if self.ns == 'rns':  # n_negs = 1
            neg_gcn_embs = item_gcn_emb[neg_item[:, :self.K]]
        else:
            neg_gcn_embs = []
            for k in range(self.K):
                neg_gcn_embs.append(self.negative_sampling(user_gcn_emb, item_gcn_emb,
                                                           user, neg_item[:, k*self.n_negs: (k+1)*self.n_negs],
                                                           pos_item))
            neg_gcn_embs = torch.stack(neg_gcn_embs, dim=1)

        return self.create_bpr_loss(user_gcn_emb[user], item_gcn_emb[pos_item], neg_gcn_embs)

    def negative_sampling(self, user_gcn_emb, item_gcn_emb, user, neg_candidates, pos_item):
        batch_size = user.shape[0]
        s_e, p_e = user_gcn_emb[user], item_gcn_emb[pos_item]  # [batch_size, n_hops+1, channel]
        if self.pool != 'concat':
            s_e = self.pooling(s_e).unsqueeze(dim=1)

        """positive mixing"""
        seed = torch.rand(batch_size, 1, p_e.shape[1], 1).to(p_e.device)  # (0, 1)
        n_e = item_gcn_emb[neg_candidates]  # [batch_size, n_negs, n_hops, channel]
        n_e_ = seed * p_e.unsqueeze(dim=1) + (1 - seed) * n_e  # mixing

        """hop mixing"""
        scores = (s_e.unsqueeze(dim=1) * n_e_).sum(dim=-1)  # [batch_size, n_negs, n_hops+1]
        indices = torch.max(scores, dim=1)[1].detach()
        neg_items_emb_ = n_e_.permute([0, 2, 1, 3])  # [batch_size, n_hops+1, n_negs, channel]
        # [batch_size, n_hops+1, channel]
        return neg_items_emb_[[[i] for i in range(batch_size)],
                              range(neg_items_emb_.shape[1]), indices, :]

    def pooling(self, embeddings):
        # [-1, n_hops, channel]
        if self.pool == 'mean':
            return embeddings.mean(dim=1)
        elif self.pool == 'sum':
            return embeddings.sum(dim=1)
        elif self.pool == 'concat':
            return embeddings.view(embeddings.shape[0], -1)
        else:  # final
            return embeddings[:, -1, :]

    def generate(self, split=True):
        user_gcn_emb, item_gcn_emb = self.gcn(self.user_embed,
                                              self.item_embed,
                                              edge_dropout=False,
                                              mess_dropout=False)
        user_gcn_emb, item_gcn_emb = self.pooling(user_gcn_emb), self.pooling(item_gcn_emb)
        if split:
            return user_gcn_emb, item_gcn_emb
        else:
            return torch.cat([user_gcn_emb, item_gcn_emb], dim=0)

    def rating(self, u_g_embeddings=None, i_g_embeddings=None):
        return torch.matmul(u_g_embeddings, i_g_embeddings.t())

    def create_bpr_loss(self, user_gcn_emb, pos_gcn_embs, neg_gcn_embs):
        # user_gcn_emb: [batch_size, n_hops+1, channel]
        # pos_gcn_embs: [batch_size, n_hops+1, channel]
        # neg_gcn_embs: [batch_size, K, n_hops+1, channel]

        batch_size = user_gcn_emb.shape[0]

        u_e = self.pooling(user_gcn_emb)
        pos_e = self.pooling(pos_gcn_embs)
        neg_e = self.pooling(neg_gcn_embs.view(-1, neg_gcn_embs.shape[2], neg_gcn_embs.shape[3])).view(batch_size, self.K, -1)

        pos_scores = torch.sum(torch.mul(u_e, pos_e), axis=1)
        neg_scores = torch.sum(torch.mul(u_e.unsqueeze(dim=1), neg_e), axis=-1)  # [batch_size, K]

        mf_loss = torch.mean(torch.log(1+torch.exp(neg_scores - pos_scores.unsqueeze(dim=1)).sum(dim=1)))

        # cul regularizer
        regularize = (torch.norm(user_gcn_emb[:, 0, :]) ** 2
                       + torch.norm(pos_gcn_embs[:, 0, :]) ** 2
                       + torch.norm(neg_gcn_embs[:, :, 0, :]) ** 2) / 2  # take hop=0
        emb_loss = self.decay * regularize / batch_size

        return mf_loss + emb_loss, mf_loss, emb_loss

LightGCN

research paper

Architecture​

Implementation​

PyTorch Implementation​

Links​

Architecture

Implementation

PyTorch Implementation

Links