GAT
GAT stands for Graph Attention Networks. This is a special GNN model that addresses several key challenges of spectral models, such as poor ability of generalization from a specific graph structure to another and sophisticated computation of matrix inverse. GAT utilizes attention mechanisms to aggregate neighborhood features (embeddings) by specifying different weights to different nodes.
research paper
We present graph attention networks (GATs), novel neural network architectures that operate on graph-structured data, leveraging masked self-attentional layers to address the shortcomings of prior methods based on graph convolutions or their approximations. By stacking layers in which nodes are able to attend over their neighborhoods' features, we enable (implicitly) specifying different weights to different nodes in a neighborhood, without requiring any kind of costly matrix operation (such as inversion) or depending on knowing the graph structure upfront. In this way, we address several key challenges of spectral-based graph neural networks simultaneously, and make our model readily applicable to inductive as well as transductive problems. Our GAT models have achieved or matched state-of-the-art results across four established transductive and inductive graph benchmarks: the Cora, Citeseer and Pubmed citation network datasets, as well as a protein-protein interaction dataset (wherein test graphs remain unseen during training).
GATs work on graph data. A graph consists of nodes and edges connecting nodes. For example, in Cora dataset the nodes are research papers and the edges are citations that connect the papers.
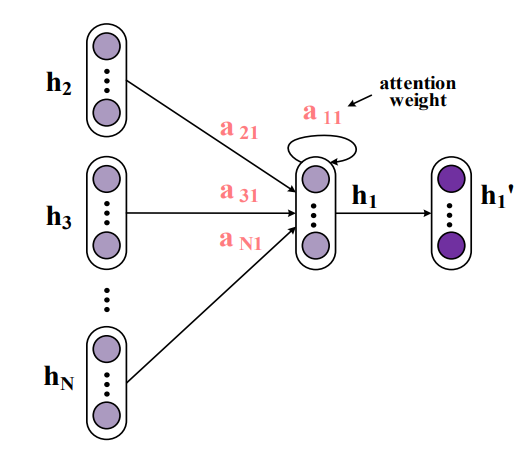
GAT uses masked self-attention, kind of similar to transformers. GAT consists of graph attention layers stacked on top of each other. Each graph attention layer gets node embeddings as inputs and outputs transformed embeddings. The node embeddings pay attention to the embeddings of other nodes it’s connected to.
The idea is to compute the hidden representations of each node in the graph, by attending over its neighbors, following a self-attention strategy. The attention architecture has several interesting properties: (1) the operation is efficient, since it is parallelizable across node neighbor pairs; (2) it can be applied to graph nodes having different degrees by specifying arbitrary weights to the neighbors; and (3) the model is directly applicable to inductive learning problems, including tasks where the model has to generalize to completely unseen graphs.
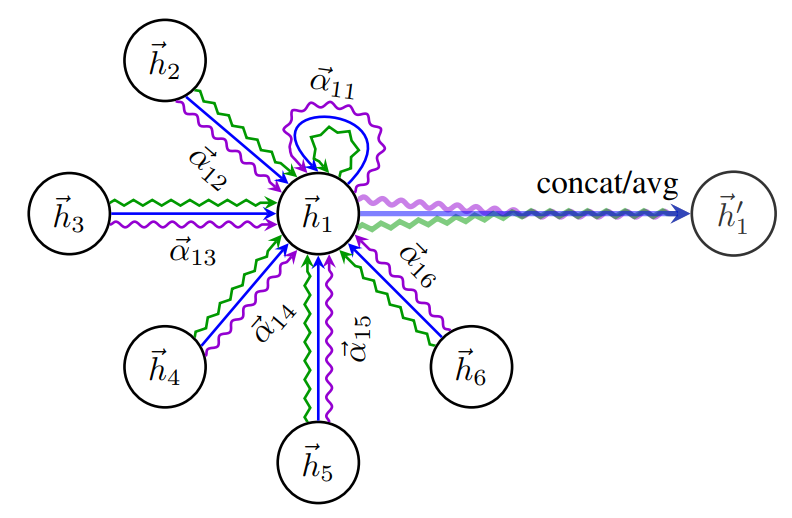
An illustration of multi-head attention (with K = 3 heads) by node 1 on its neighborhood. Different arrow styles and colors denote independent attention computations. The aggregated features from each head are concatenated or averaged to obtain .
Formally,
To stabilize the learning process of self-attention, we have found extending our mechanism to employ multi-head attention to be beneficial, similarly to Vaswani et al. (2017). Specifically, K independent attention mechanisms execute the transformation, and then their features are concatenated, resulting in the following output feature representation:
If we perform multi-head attention on the final (prediction) layer of the network, concatenation is no longer sensible—instead, we employ averaging, and delay applying the final nonlinearity (usually a softmax or logistic sigmoid for classification problems) until then.

A t-SNE plot of the computed feature representations of a pre-trained GAT model’s first hidden layer on the Cora dataset. Node colors denote classes. Edge thickness indicates aggregated normalized attention coefficients between nodes i and j, across all eight attention heads (\sum{k=1}^K \alpha{ij}^k + \alpha{ji}^k).
GATv2
Abstract
Graph Attention Networks (GATs) are one of the most popular GNN architectures and are considered as the state-of-the-art architecture for representation learning with graphs. In GAT, every node attends to its neighbors given its own representation as the query. However, in this paper we show that GATs can only compute a restricted kind of attention where the ranking of attended nodes is unconditioned on the query node. We formally define this restricted kind of attention as static attention and distinguish it from a strictly more expressive dynamic attention. Because GATs use a static attention mechanism, there are simple graph problems that GAT cannot express: in a controlled problem, we show that static attention hinders GAT from even fitting the training data. To remove this limitation, we introduce a simple fix by modifying the order of operations and propose GATv2: a dynamic graph attention variant that is strictly more expressive than GAT. We perform an extensive evaluation and show that GATv2 outperforms GAT across 11 OGB and other benchmarks while we match their parametric costs.
GATv2s work on graph data similar to GAT. A graph consists of nodes and edges connecting nodes. For example, in Cora dataset the nodes are research papers and the edges are citations that connect the papers.
The GATv2 operator fixes the static attention problem of the standard GAT. Static attention is when the attention to the key nodes has the same rank (order) for any query node.