GRU4Rec
It uses session-parallel mini-batch approach where we first create an order for the sessions and then, we use the first event of the first X sessions to form the input of the first mini-batch (the desired output is the second events of our active sessions). The second mini-batch is formed from the second events and so on. If any of the sessions end, the next available session is put in its place. Sessions are assumed to be independent, thus we reset the appropriate hidden state when this switch occurs.
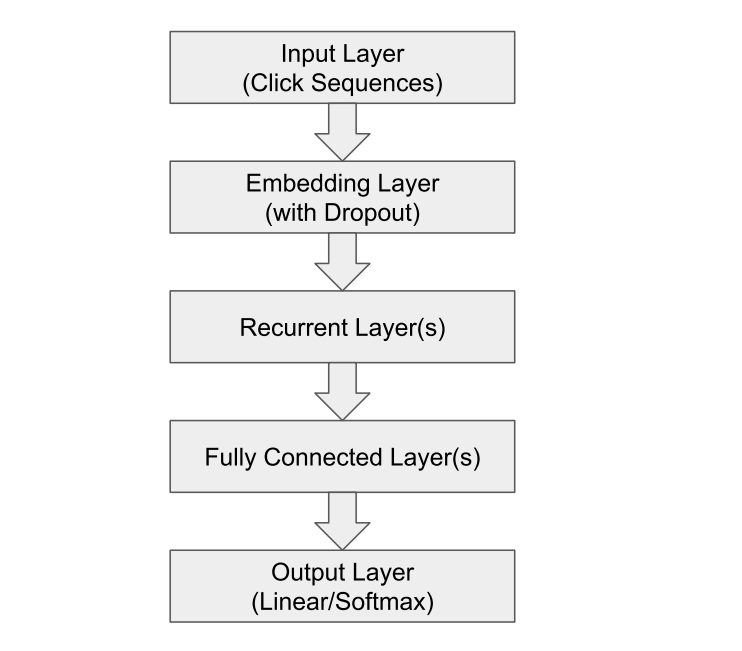
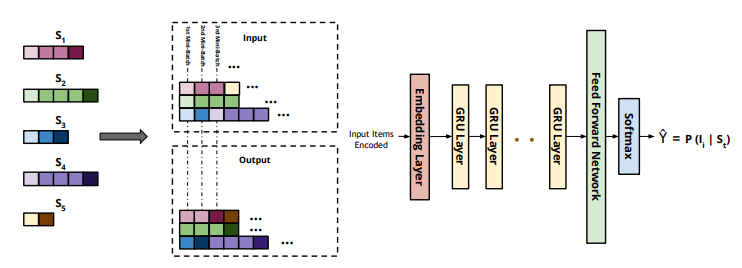
One of the first successful approaches for using RNNs in the recommendation domain is the GRU4Rec network (Hidasi, Karatzoglou, Baltrunas, and Tikk, 2015). A RNN with GRUs was used for the session-based recommendation. A novel training mechanism called session-parallel mini-batches is used in GRU4Rec, as shown in Figure 3. Each position in a mini-batch belongs to a particular session in the training data. The network finds a hidden state for each position in the batch separately, but this hidden state is kept and used in the next iteration at the positions when the same session continues with the next batch. However, it is erased at the positions of new sessions coming up with the start of the next batch. The network is always updated with the session beginning and used to predict the subsequent events. GRU4Rec architecture is composed of an embedding layer followed by multiple optional GRU layers, a feed-forward network, and a softmax layer for output score predictions for candidate items. The session items are one-hot-encoded in a vector representing all items’ space to be fed into the network as input. On the other hand, a similar output vector is obtained from the softmax layer to represent the predicted ranking of items. Additionally, the authors designed two new loss functions, namely, Bayesian personalized ranking (BPR) loss and regularized approximation of the relative rank of the relevant item (TOP1) loss. BPR uses a pairwise ranking loss function by averaging the target item’s score with several sampled negative ones in the loss value. TOP1 is the regularized approximation of the relative rank of the relevant item loss. Later, Hidasi and Karatzoglou (2018) extended their work by modifying the two-loss functions introduced previously by solving the issues of vanishing gradient faced by TOP1 and BPR when the negative samples have very low predicted likelihood that approaches zero. The newly proposed losses merge between the knowledge from the deep learning and the literature of learning to rank. The evaluation of the new extended version shows a clear superiority over the older version of the network. Thus, we have included the extended version of the GRU4Rec network, denoted by GRU4Rec+, in our evaluation study.