MF

Matrix Factorization is an iterative approach of SVD called Regularized SVD. It uses the gradient-descent method to estimate the resulting matrices. The obtained model will not be a true SVD of the rating-matrix, as the component matrices are no longer orthogonal, but tends to be more accurate at predicting unseen preferences than the standard SVD [Ekstrand et al. 2011].

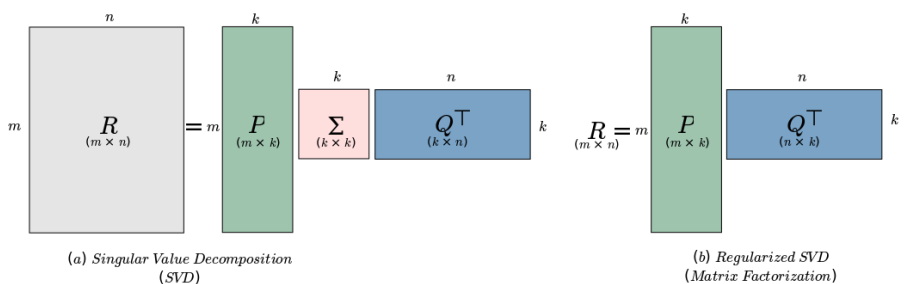
MF represents both users and items in a common, low-dimensional latent-space by factorizing the user-item interaction matrix. Formally, the rating/relevance for user 𝑢 and item 𝑖 is modeled as $\hat{r}_i^u = \alpha + \beta_u + \beta_i + \gamma_u \cdot \gamma_i$ where $\gamma_u , \gamma_i \in \mathbb{R}^d$ are learned latent representations.