HMLET

HMLET stands for Hybrid Method of Linear and nonlinEar collaborative filTering (HMLET, pronounced as Hamlet). It is a GCN-based CF method.

research paper

Kong et. al., “Linear, or Non-Linear, That is the Question!”. WSDM, 2022.

There were fierce debates on whether the non-linear embedding propagation of GCNs is appropriate to GCN-based recommender systems. It was recently found that the linear embedding propagation shows better accuracy than the non-linear embedding propagation. Since this phenomenon was discovered especially in recommender systems, it is required that we carefully analyze the linearity and non-linearity issue. In this work, therefore, we revisit the issues of i) which of the linear or non-linear propagation is better and ii) which factors of users/items decide the linearity/non-linearity of the embedding propagation. We propose a novel Hybrid Method of Linear and non-linEar collaborative filTering method (HMLET, pronounced as Hamlet). In our design, there exist both linear and non-linear propagation steps, when processing each user or item node, and our gating module chooses one of them, which results in a hybrid model of the linear and non-linear GCN-based collaborative filtering (CF). The proposed model yields the best accuracy in three public benchmark datasets. Moreover, we classify users/items into the following three classes depending on our gating modules' selections: Full-Non-Linearity (FNL), Partial-Non-Linearity (PNL), and Full-Linearity (FL). We found that there exist strong correlations between nodes' centrality and their class membership, i.e., important user/item nodes exhibit more preferences towards the non-linearity during the propagation steps. To our knowledge, we are the first who designs a hybrid method and reports the correlation between the graph centrality and the linearity/non-linearity of nodes. All HMLET codes and datasets are available at: this https URL.

There are four variants of HMLET in terms of the location of the non-linear propagation. HMLET(End) shows the best accuracy in experiments. It was known that the problem of over-smoothing happens with more than 2 non-linear propagation layers, and therefore we are using up to 2 non-linear layers.

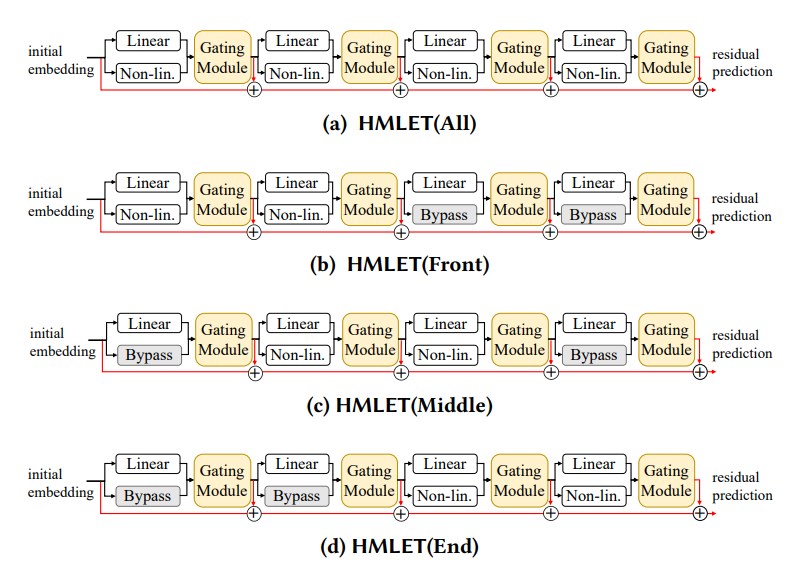
Each method except HMLET(All) uses up to 2 non-linear layers since it is known that more than 2 non-linear layers cause the problem of over-smoothing. Moreover, we test with various options of where to put them. First, HMLET(Front) focuses on the fact that GCNs are highly influenced by close neighborhood, i.e., in the first and second layers. Therefore, HMLET(Front) adopts the gating module in the front and uses only the linear propagation layers afterwards. Second, HMLET(Middle) only uses the linear propagation in the front and last and then adopts the gating module in the second and third layers. Last, as the gating module is located in the third and fourth layers, HMLET(End) focuses on gating in the third and fourth layers.

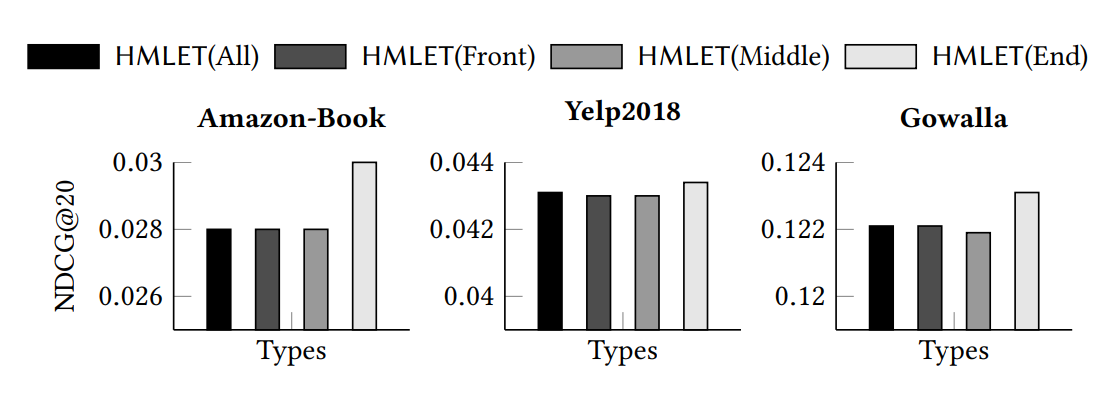
The comparison of NDCG@20 with all types of HMLET in three public benchmarks.

Note: We will focus on HMLET (end) variant, as it shows the superior performance on the above three public datasets.

Architecture

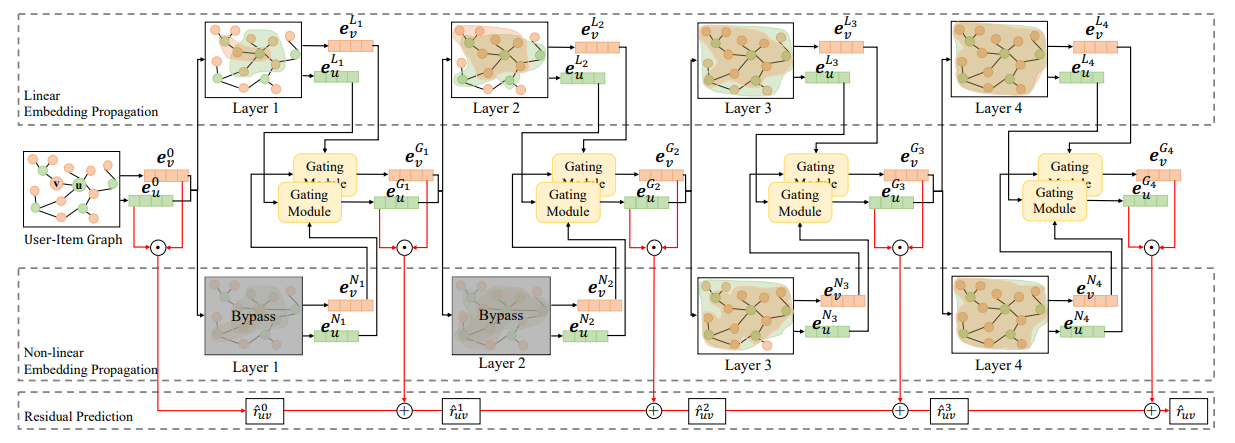
The detailed workflow of HMLET(End). This model variant bypasses the nonlinearity propagation on the first and second layers to address the over-smoothing problem and then propagates the non-linear embedding in the third and fourth layers. We prepare both the linear and non-linear propagation steps in a layer and let our gating module with STGS (straight-through Gumbel softmax) decide which one to use for each node. For instance, it can select a sequence of linear → linear → linear → non-linear for some nodes while it can select a totally different sequence for other nodes.