Skip to main content

FGNN

research paper

Ruihong Qiu, Jingjing Li, Zi Huang and Hongzhi Yin, “Rethinking the Item Order in Session-based Recommendation with Graph Neural Networks”. CIKM, 2019.

Predicting a user's preference in a short anonymous interaction session instead of long-term history is a challenging problem in the real-life session-based recommendation, e.g., e-commerce and media stream. Recent research of the session-based recommender system mainly focuses on sequential patterns by utilizing the attention mechanism, which is straightforward for the session's natural sequence sorted by time. However, the user's preference is much more complicated than a solely consecutive time pattern in the transition of item choices. In this paper, therefore, we study the item transition pattern by constructing a session graph and propose a novel model which collaboratively considers the sequence order and the latent order in the session graph for a session-based recommender system. We formulate the next item recommendation within the session as a graph classification problem. Specifically, we propose a weighted attention graph layer and a Readout function to learn embeddings of items and sessions for the next item recommendation. Extensive experiments have been conducted on two benchmark E-commerce datasets, Yoochoose and Diginetica, and the experimental results show that our model outperforms other state-of-the-art methods.

Architecture​

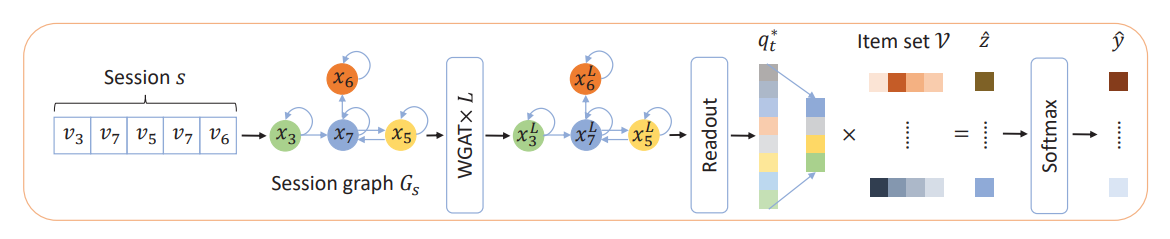
Pipeline of FGNN. The input to the model is organized as a session sequence s, which is then converted to a session graph $G$ with node features $x$. $L$ layers of WGAT serves as the encoder of node features for $G$. After being processed by WGAT, the session graph now contains different semantic node representations $x^L$ but with the same structure as the input session graph. The Readout function is applied to generate a session embedding based on the learned node features. Compared with other items in the item set $mathcal{V}$, a recommendation score $hat{y}_i$ is finally generated.

Pipeline of FGNN. The input to the model is organized as a session sequence s, which is then converted to a session graph GG with node features xx. LL layers of WGAT serves as the encoder of node features for GG. After being processed by WGAT, the session graph now contains different semantic node representations xLx^L but with the same structure as the input session graph. The Readout function is applied to generate a session embedding based on the learned node features. Compared with other items in the item set V\mathcal{V}, a recommendation score y^i\hat{y}_i is finally generated.

At the first stage, the session sequence is converted into a session graph for the purpose to process each session via GNN. Because of the natural order of the session sequence, we transform it into a weighted directed graph, GsG_s. The weight of the edge is defined as the frequency of the occurrence of the edge within the session. If a node does not contain a self loop, it will be added with a self loop with a weight 1. Based on our observation of our daily life and the datasets, it is common for a user to click two consecutive items for a few times within the session. After converting the session into a graph, the final embedding of SS is based on the calculation on this session graph GsG_s.

After obtaining the session graph, a GNN is needed to learn embeddings for nodes in a graph, which is the WGAT × LL part in figure. In recent years, some baseline methods on GNN, for example, GCN and GAT, are demonstrated to be capable of extracting features of the graph. However, most of them are only well-suited for unweighted and undirected graphs. For the session graph, weighted and directed, these baseline methods cannot be directly applied without losing the information carried by the weighted directed edge. Therefore, a suitable graph convolutional layer is needed to effectively convey information between the nodes in the graph. A weighted graph attentional layer (WGAT) simultaneously incorporates the edge weight when performing the attention aggregation on neighboring nodes.

To learn the node representation via the higher order item transition pattern within the graph structure, a self-attention mechanism for every node ii is used to aggregate information from its neighboring nodes N(i)\mathcal{N}(i), which is defined as the nodes with edges towards the node ii (may contain ii itself if there is a self-loop edge). Because the size of the session graph is not huge, we can take the entire neighborhood of a node into consideration without any sampling.

A Readout function aims to give out a representation of the whole graph based on the node features after the forward computation of the GNN layers. The Readout function needs to learn the order of the item transition pattern to avoid the bias of the time order and the inaccuracy of the self-attention on the last input item. For the convenience, some algorithms use simple permutation invariant operations for example, mean, max, or sum over all node features.

References​