DGTN

DGTN stands for Dual-channel Graph Transition Network.

research paper

Zheng et. al., “Dual-channel Graph Transition Network for Session-based Recommendation”. arXiv, 2020.

The task of session-based recommendation is to predict user actions based on anonymous sessions. Recent research mainly models the target session as a sequence or a graph to capture item transitions within it, ignoring complex transitions between items in different sessions that have been generated by other users. These item transitions include potential collaborative information and reflect similar behavior patterns, which we assume may help with the recommendation for the target session. In this paper, we propose a novel method, namely Dual-channel Graph Transition Network (DGTN), to model item transitions within not only the target session but also the neighbor sessions. Specifically, we integrate the target session and its neighbor (similar) sessions into a single graph. Then the transition signals are explicitly injected into the embedding by channel-aware propagation. Experiments on real-world datasets demonstrate that DGTN outperforms other state-of-the-art methods. Further analysis verifies the rationality of dual-channel item transition modeling, suggesting a potential future direction for session-based recommendation.

Architecture

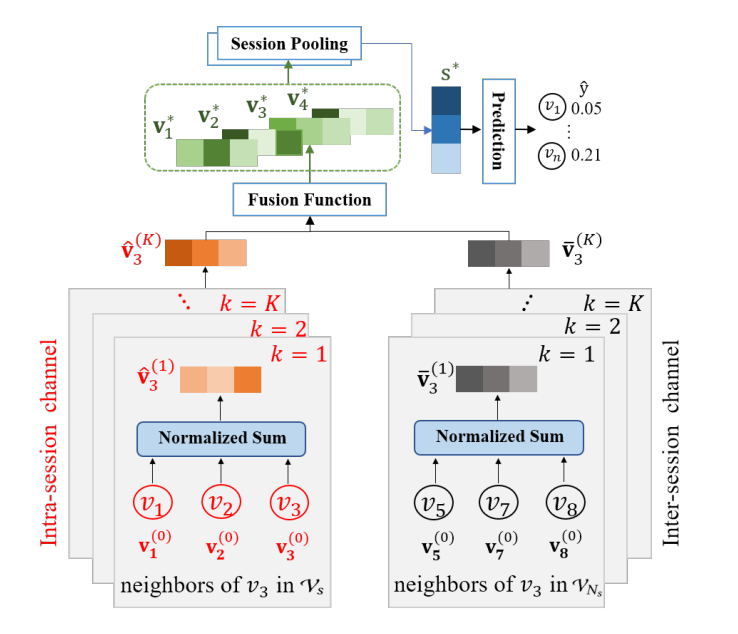
An illustration of the model architecture. Taking item $v_3$ for example, we propagate the embeddings of neighbor items in the target session $s$ and the neighbor session set $N_s$ towards the next layer in the intra- and intersession channel, respectively. Then the embeddings of the final layer in the two channels are fed into the fusion function to obtain the final item embedding $v_3^*$. Based on the learned item embeddings, we generate the session embedding via session pooling. Finally, we apply a prediction layer to generate the recommendation probability $\hat{y}$.

Given a session $s$, we first determine its neighbor set $N_s$ consisting of its $r$ most similar previous sessions. To simplify the computation, we use the number of duplicate items between sessions to calculate the similarity. Based on the ranking of the number of duplicate items between each session and the target session, we sample the top-$r$ sessions to constitute the neighborhood set $N_s$. Then we model the target session $s$ and its neighbor sessions in $N_s$ as a session graph $G_s$, where each node represents either an item that appears in the session $s$ or any neighbor session in $N_s$. Each edge $(v_i , v_j)$ denotes a user clicking on item $v_j$ after $v_i$ in the session $s$ or any neighbor session in $N_s$.

To encode the item transition signals into item embeddings, we follow the message-passing structure of GNN. Each item node $v_i$ in the graph aggregates messages passed from its neighbor item nodes in the graph. However, the constructed session graph contains item nodes from target session $s$ and neighbor sessions $N_s$, which reflect the users’ current behaviors and the global collaborative information, respectively. They ought to have different effects on the recommendation. Therefore, we propagate the item embeddings in two channels for the two types of neighbor item nodes. In the intra-session channel, we aggregate messages from only the neighbor nodes in $V_s$. In the inter-session channel, we aggregate messages from the neighbor nodes in $V_{N_s}$.

Only the normalized sum of neighbor embeddings are propagated towards next layers:

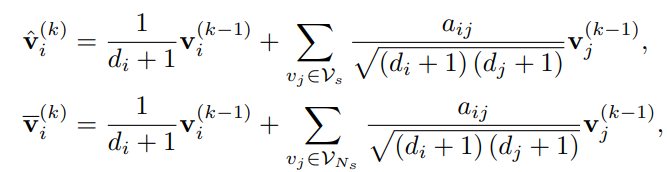
where $d_i$ is the degree of node $v_i$ in the adjacency matrix. $a_{ij}$ = 1 denotes that there is an edge between node $v_i$ and $v_j$, and a missing edge is represented through $a_{ij}$ = 0.

Then we need to fuse the information of these two channels together and extract effective features. We exploy CNN pooling method for this.

We combine both users’ long-term preference and short-term interests of the session to generate the final session embedding. For the session $s = \{v_1, v_2, \dots, v_n\}$, we use the last click item’s embedding to represent user’s short-term interests. Then we obtain the long-term preference by adopting a soft-attention mechanism to draw dependencies between the short-term interest and each item in the session.