LIRD
Existing reinforcement learning recommender methods also could recommend a list of items. E.g. DQN can calculate Q-values of all recalled items separately, and recommend a list of items with highest Q-values. But these recommendations are similar in Euclidean space and we want to find similarity in associative space. For instance, for a bread 🍞, I want egg 🥚, milk 🥛 in my recommendation list instead of white bread 🍞, brown bread 🥪, bun 🫓 etc.
Therefore, in this framework, we will see a principled approach to capture relationship among recommended items and generate a list of complementary items to enhance the performance.
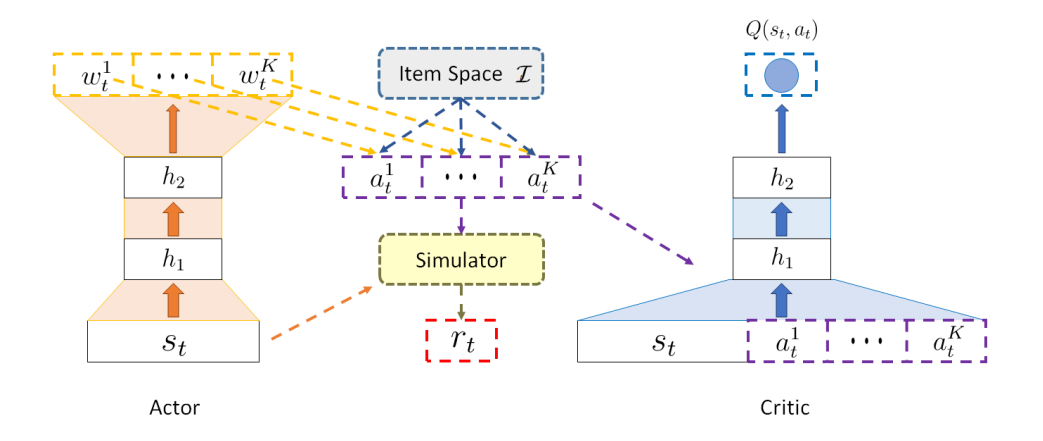
The Actor network
The Actor first generates a list of weight vectors. For each weight vector, the RA scores all items in the item space, selects the item with highest score, and then adds this item at the end of the recommendation list. Finally the RA removes this item from the item space, which prevents recommending the same item to the recommendation list.
Implementation in Tensorflow 1.0
class Actor(object):
"""policy function approximator"""
def __init__(self, sess, s_dim, a_dim, batch_size, output_size, weights_len, tau, learning_rate, scope="actor"):
self.sess = sess
self.s_dim = s_dim
self.a_dim = a_dim
self.batch_size = batch_size
self.output_size = output_size
self.weights_len = weights_len
self.tau = tau
self.learning_rate = learning_rate
self.scope = scope
with tf.variable_scope(self.scope):
# estimator actor network
self.state, self.action_weights, self.len_seq = self._build_net("estimator_actor")
self.network_params = tf.trainable_variables()
# self.network_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='estimator_actor')
# target actor network
self.target_state, self.target_action_weights, self.target_len_seq = self._build_net("target_actor")
self.target_network_params = tf.trainable_variables()[len(self.network_params):]
# self.target_network_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='target_actor')
# operator for periodically updating target network with estimator network weights
self.update_target_network_params = [
self.target_network_params[i].assign(
tf.multiply(self.network_params[i], self.tau) +
tf.multiply(self.target_network_params[i], 1 - self.tau)
) for i in range(len(self.target_network_params))
]
self.hard_update_target_network_params = [
self.target_network_params[i].assign(
self.network_params[i]
) for i in range(len(self.target_network_params))
]
self.a_gradient = tf.placeholder(tf.float32, [None, self.a_dim])
self.params_gradients = list(
map(
lambda x: tf.div(x, self.batch_size * self.a_dim),
tf.gradients(tf.reshape(self.action_weights, [self.batch_size, self.a_dim]),
self.network_params, -self.a_gradient)
)
)
self.optimizer = tf.train.AdamOptimizer(self.learning_rate).apply_gradients(
zip(self.params_gradients, self.network_params)
)
self.num_trainable_vars = len(self.network_params) + len(self.target_network_params)
@staticmethod
def cli_value(x, v):
y = tf.constant(v, shape=x.get_shape(), dtype=tf.int64)
return tf.where(tf.greater(x, y), x, y)
def _gather_last_output(self, data, seq_lens):
this_range = tf.range(tf.cast(tf.shape(seq_lens)[0], dtype=tf.int64), dtype=tf.int64)
tmp_end = tf.map_fn(lambda x: self.cli_value(x, 0), seq_lens - 1, dtype=tf.int64)
indices = tf.stack([this_range, tmp_end], axis=1)
return tf.gather_nd(data, indices)
def _build_net(self, scope):
"""build the tensorflow graph"""
with tf.variable_scope(scope):
state = tf.placeholder(tf.float32, [None, self.s_dim], "state")
state_ = tf.reshape(state, [-1, self.weights_len, int(self.s_dim / self.weights_len)])
len_seq = tf.placeholder(tf.int32, [None])
cell = tf.nn.rnn_cell.GRUCell(self.output_size,
activation=tf.nn.relu,
kernel_initializer=tf.initializers.random_normal(),
bias_initializer=tf.zeros_initializer())
outputs, _ = tf.nn.dynamic_rnn(cell, state_, dtype=tf.float32, sequence_length=len_seq)
outputs = self._gather_last_output(outputs, len_seq)
return state, outputs, len_seq
def train(self, state, a_gradient, len_seq):
self.sess.run(self.optimizer, feed_dict={self.state: state, self.a_gradient: a_gradient, self.len_seq: len_seq})
def predict(self, state, len_seq):
return self.sess.run(self.action_weights, feed_dict={self.state: state, self.len_seq: len_seq})
def predict_target(self, state, len_seq):
return self.sess.run(self.target_action_weights, feed_dict={self.target_state: state,
self.target_len_seq: len_seq})
def update_target_network(self):
self.sess.run(self.update_target_network_params)
def hard_update_target_network(self):
self.sess.run(self.hard_update_target_network_params)
def get_num_trainable_vars(self):
return self.num_trainable_vars
Implementation in PyTorch
class Actor(nn.Module):
def __init__(self, input_size,input_sequence_length, output_sequence_length, output_size):
super(Actor, self).__init__()
self.weight_matrix = torch.nn.Parameter(torch.ones((1,input_sequence_length), requires_grad=True))
self.Linear = nn.Linear(input_size, output_size)
self.Activation = nn.Softmax(dim=-1)
self.output_shape = (output_sequence_length,output_size)
def forward(self, state):
"""
Param state is a torch tensor
"""
state = torch.FloatTensor(state)
size = len(state.shape)
if size==2:
state = state.unsqueeze(0)
state = self.weight_matrix.matmul(state)
state = state.squeeze(1)
action = []
# x = self.Linear(state)
action.append(self.Activation(state))
for i in range(self.output_shape[0]-1):
indices = action[i].argmax(-1).unsqueeze(-1)
action_i = action[i].scatter(-1,indices,0)
action_i = action_i / action_i.sum(-1).unsqueeze(-1)
action.append(action_i)
action = torch.cat(action,-1).reshape((-1,self.output_shape[0],self.output_shape[1]))
if size==2:
action = action.squeeze(0)
return action
Online User-Agent Interaction Environment Simulator
In the online recommendation procedure, given the current state st , the RA recommends a list of items at to a user, and the user browses these items and provides her feedbacks, i.e., skip/click/order part of the recommended items. The RA receives immediate reward r(st , at ) according to the user’s feedback. To tackle the challenge of training and evaluating the performance of the framework offline, we will simulate the aforementioned online interaction procedures, The task of simulator is to predict a reward based on current state and a selected action, i.e., .
Implementation in Python
class Simulator(object):
def __init__(self, alpha=0.5, sigma=0.9):
self.data = data
self.alpha = alpha
self.sigma = sigma
self.init_state = self.reset()
self.current_state = self.init_state
self.rewards, self.group_sizes, self.avg_states, self.avg_actions = self.avg_group()
def reset(self):
init_state = np.array(self.data['state_float'].sample(1).values[0]).reshape((1, 12, 30))
self.current_state = init_state
return init_state
def step(self, action):
simulate_rewards, result = self.simulate_reward((self.current_state.reshape((1, 360)),
action.reshape((1, 120))))
for i, r in enumerate(simulate_rewards.split('|')):
if r != "show":
# self.current_state.append(action[i])
tmp = np.append(self.current_state[0], action[i].reshape((1, 30)), axis=0)
tmp = np.delete(tmp, 0, axis=0)
self.current_state = tmp[np.newaxis, :]
return result, self.current_state
def avg_group(self):
"""calculate average state/action value for each group."""
rewards = list()
avg_states = list()
avg_actions = list()
group_sizes = list()
for reward, group in self.data.groupby(['reward']):
n_size = group.shape[0]
state_values = group['state_float'].values.tolist()
action_values = group['action_float'].values.tolist()
avg_states.append(
np.sum(state_values / np.linalg.norm(state_values, 2, axis=1)[:, np.newaxis], axis=0) / n_size
)
avg_actions.append(
np.sum(action_values / np.linalg.norm(action_values, 2, axis=1)[:, np.newaxis], axis=0) / n_size
)
group_sizes.append(n_size)
rewards.append(reward)
return rewards, group_sizes, avg_states, avg_actions
def simulate_reward(self, pair):
"""use the average result to calculate simulated reward.
Args:
pair (tuple): <state, action> pair
Returns:
simulated reward for the pair.
"""
probability = list()
denominator = 0.
max_prob = 0.
result = 0.
simulate_rewards = ""
# change a different way to calculate simulated reward
for s, a, r in zip(self.avg_states, self.avg_actions, self.rewards):
numerator = self.alpha * (
np.dot(pair[0], s)[0] / (np.linalg.norm(pair[0], 2) * np.linalg.norm(s, 2))
) + (1 - self.alpha) * (
np.dot(pair[1], a)[0] / (np.linalg.norm((pair[1], 2) * np.linalg.norm(a, 2)))
)
probability.append(numerator)
denominator += numerator
if numerator > max_prob:
max_prob = numerator
simulate_rewards = r
probability /= denominator
for p, r in zip(probability, self.rewards):
for k, reward in enumerate(r.split('|')):
result += p * np.power(self.sigma, k) * (0 if reward == "show" else 1)
# calculate simulated reward by group
# for i, reward in enumerate(self.rewards):
# numerator = self.group_sizes[i] * (
# self.alpha * (np.dot(pair[0], self.avg_states[i])[0] / np.linalg.norm(pair[0], 2)) +
# (1 - self.alpha) * (np.dot(pair[1], self.avg_actions[i]) / np.linalg.norm(pair[1], 2))
# )
# probability.append(numerator)
# denominator += numerator
# probability /= denominator
# # max probability
# simulate_rewards = self.rewards[int(np.argmax(probability))]
# calculate simulated reward in normal way
# for idx, row in data.iterrows():
# state_values = row['state_float']
# action_values = row['action_float']
# numerator = self.alpha * (
# np.dot(pair[0], state_values)[0] / (np.linalg.norm(pair[0], 2) * np.linalg.norm(state_values, 2))
# ) + (1 - self.alpha) * (
# np.dot(pair[1], action_values)[0] / (np.linalg.norm(pair[1], 2) * np.linalg.norm(action_values, 2))
# )
# probability.append(numerator)
# denominator += numerator
# probability /= denominator
# simulate_rewards = data.iloc[int(np.argmax(probability))]['reward']
# for k, reward in enumerate(simulate_rewards.split('|')):
# result += np.power(self.sigma, k) * (0 if reward == "show" else 1)
return simulate_rewards, result
The Critic network
The Critic is designed to leverage an approximator to learn an action-value function , which is a judgment of whether the action at generated by Actor matches the current state . Then, according , the Actor updates its’ parameters in a direction of improving performance to generate proper actions in the following iterations. Many applications in reinforcement learning make use of the optimal action-value function . It is the maximum expected return achievable by the optimal policy, and should follow the Bellman equation. In practice, the action-value function is usually highly nonlinear. Deep neural networks are known as excellent approximators for nonlinear functions. In this paper, We refer to a neural network function approximator with parameters as deep Q-network (DQN). A DQN can be trained by minimizing a sequence of loss functions:
Implementation in PyTorch
class Critic(nn.Module):
def __init__(self, state_size, action_size, hidden_size, action_sequence_length):
super(Critic, self).__init__()
self.encode_state = nn.LSTM(state_size,action_size,batch_first = True)
hidden_stack = [nn.Linear((action_sequence_length + 1)*action_size, hidden_size),
nn.ReLU(),]
for i in range(3):
hidden_stack.extend([nn.Linear(hidden_size, hidden_size), nn.ReLU()])
self.hidden_layer = nn.Sequential(*hidden_stack)
self.output_layer = nn.Linear(hidden_size, 1)
def forward(self, state, action):
"""
Params state and actions are torch tensors
"""
if not isinstance(state,torch.Tensor):
state = torch.tensor(state)
if not isinstance(action,torch.Tensor):
action = torch.tensor(action)
if (len(state.shape)==2) and (len(action.shape)==2):
action = action.unsqueeze(0)
state = state.unsqueeze(0)
_,(encoded_state,__) = self.encode_state(state)
encoded_state = encoded_state.squeeze(0)
action = action.flatten(1)
x = torch.cat([encoded_state,action],-1)
x = self.hidden_layer(x)
x = self.output_layer(x)
if (len(state.shape)==2) and (len(action.shape)==2):
x = x.squeeze(0)
return x
Implementation in Tensorflow 1.0
class Critic(object):
"""value function approximator"""
def __init__(self, sess, s_dim, a_dim, num_actor_vars, weights_len, gamma, tau, learning_rate, scope="critic"):
self.sess = sess
self.s_dim = s_dim
self.a_dim = a_dim
self.num_actor_vars = num_actor_vars
self.weights_len = weights_len
self.gamma = gamma
self.tau = tau
self.learning_rate = learning_rate
self.scope = scope
with tf.variable_scope(self.scope):
# estimator critic network
self.state, self.action, self.q_value, self.len_seq = self._build_net("estimator_critic")
# self.network_params = tf.trainable_variables()[self.num_actor_vars:]
self.network_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope="estimator_critic")
# target critic network
self.target_state, self.target_action, self.target_q_value, self.target_len_seq = self._build_net("target_critic")
# self.target_network_params = tf.trainable_variables()[(len(self.network_params) + self.num_actor_vars):]
self.target_network_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope="target_critic")
# operator for periodically updating target network with estimator network weights
self.update_target_network_params = [
self.target_network_params[i].assign(
tf.multiply(self.network_params[i], self.tau) +
tf.multiply(self.target_network_params[i], 1 - self.tau)
) for i in range(len(self.target_network_params))
]
self.hard_update_target_network_params = [
self.target_network_params[i].assgin(
self.network_params[i]
) for i in range(len(self.target_network_params))
]
self.predicted_q_value = tf.placeholder(tf.float32, [None, 1])
self.loss = tf.reduce_mean(tf.squared_difference(self.predicted_q_value, self.q_value))
self.optimizer = tf.train.AdamOptimizer(self.learning_rate).minimize(self.loss)
self.a_gradient = tf.gradients(self.q_value, self.action)
@staticmethod
def cli_value(x, v):
y = tf.constant(v, shape=x.get_shape(), dtype=tf.int64)
return tf.where(tf.greater(x, y), x, y)
def _gather_last_output(self, data, seq_lens):
this_range = tf.range(tf.cast(tf.shape(seq_lens)[0], dtype=tf.int64), dtype=tf.int64)
tmp_end = tf.map_fn(lambda x: self.cli_value(x, 0), seq_lens - 1, dtype=tf.int64)
indices = tf.stack([this_range, tmp_end], axis=1)
return tf.gather_nd(data, indices)
def _build_net(self, scope):
with tf.variable_scope(scope):
state = tf.placeholder(tf.float32, [None, self.s_dim], "state")
state_ = tf.reshape(state, [-1, self.weights_len, int(self.s_dim / self.weights_len)])
action = tf.placeholder(tf.float32, [None, self.a_dim], "action")
len_seq = tf.placeholder(tf.int64, [None], name="critic_len_seq")
cell = tf.nn.rnn_cell.GRUCell(self.weights_len,
activation=tf.nn.relu,
kernel_initializer=tf.initializers.random_normal(),
bias_initializer=tf.zeros_initializer()
)
out_state, _ = tf.nn.dynamic_rnn(cell, state_, dtype=tf.float32, sequence_length=len_seq)
out_state = self._gather_last_output(out_state, len_seq)
inputs = tf.concat([out_state, action], axis=-1)
layer1 = tf.layers.Dense(32, activation=tf.nn.relu)(inputs)
layer2 = tf.layers.Dense(16, activation=tf.nn.relu)(layer1)
q_value = tf.layers.Dense(1)(layer2)
return state, action, q_value, len_seq
def train(self, state, action, predicted_q_value, len_seq):
return self.sess.run([self.q_value, self.loss, self.optimizer], feed_dict={
self.state: state,
self.action: action,
self.predicted_q_value: predicted_q_value,
self.len_seq: len_seq
})
def predict(self, state, action, len_seq):
return self.sess.run(self.q_value, feed_dict={self.state: state, self.action: action, self.len_seq: len_seq})
def predict_target(self, state, action, len_seq):
return self.sess.run(self.target_q_value, feed_dict={self.target_state: state, self.target_action: action,
self.len_seq: len_seq})
def action_gradients(self, state, action, len_seq):
return self.sess.run(self.a_gradient, feed_dict={self.state: state, self.action: action, self.len_seq: len_seq})
def update_target_network(self):
self.sess.run(self.update_target_network_params)
def hard_update_target_network(self):
self.sess.run(self.hard_update_target_network_params)
The Training Procedure
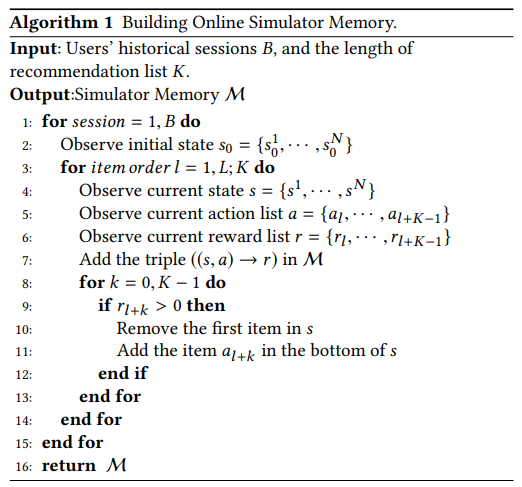
We utilize DDPG algorithm to train the parameters. In each iteration, there are two stages, i.e., 1) transition generating stage (lines 8-20), and 2) parameter updating stage (lines 21-28). For transition generating stage (line 8): given the current state , the RA first recommends a list of items (line 9); then the agent observes the reward from simulator (line 10) and updates the state to (lines 11-17); and finally the recommender agent stores transitions into the memory (line 19), and set (line 20).

For parameter updating stage: the recommender agent samples mini-batch of transitions from (line 22), and then updates parameters of Actor and Critic (lines 23-28) following a standard DDPG procedure. In the algorithm, we introduce widely used techniques to train our framework. For example, we utilize a technique known as experience replay (lines 3,22), and introduce separated evaluation and target networks (lines 2,23), which can help smooth the learning and avoid the divergence of parameters. For the soft target updates of target networks (lines 27,28), we used τ = 0.001. Moreover, we leverage prioritized sampling strategy to assist the framework learning from the most important historical transitions.
The Testing Procedure
After framework training stage, RA gets well-trained parameters, say and . Then we can do framework testing on simulator environment. The model testing also follows the above algorithm, i.e., the parameters continuously updates during the testing stage, while the major difference from training stage is before each recommendation session, we reset the parameters back to and for the sake of fair comparison between each session. We can artificially control the length of recommendation session to study the short-term and long-term performance.