DeepWalk

DeepWalk learns representations of online social networks graphs. By performing random walks to generate sequences, the paper demonstrated that it was able to learn vector representations of nodes (e.g., profiles, content) in the graph.

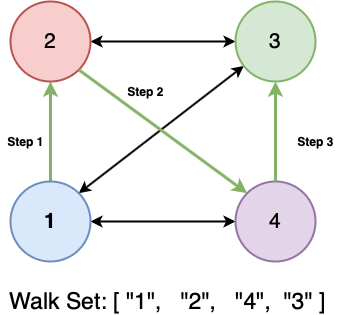
/img/content-models-raw-mp2-deepwalk-untitled.png

The DeepWalk process operates in a few steps

For each node, perform N “random steps” starting from that node
Treat each walk as a sequence of node-id strings
Given a list of these sequences, train a word2vec model using the Skip-Gram algorithm on these string sequences

Let's see how it works in depth

node embedding learned in an unsupervised manner

/img/content-models-raw-mp2-deepwalk-untitled-1.png

highly resembles word embedding in terms of the training process
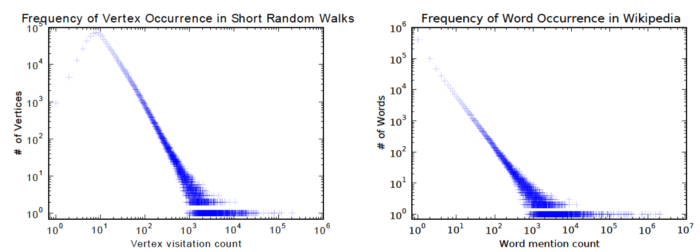
motivation is that the distribution of both nodes in a graph and words in a corpus follow a power law
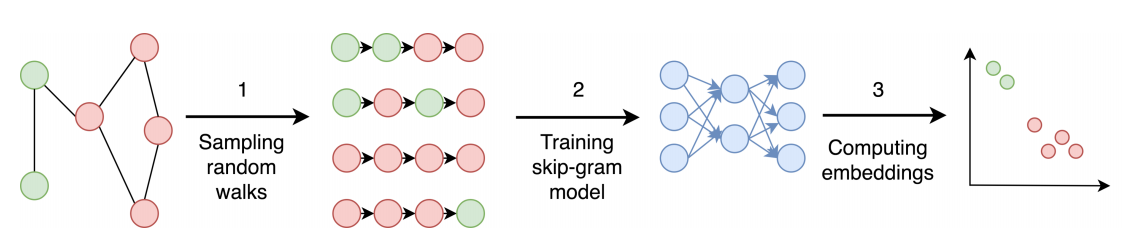
The algorithm contains two steps: 1) Perform random walks on nodes in a graph to generate node sequences, 2) Run skip-gram to learn the embedding of each node based on the node sequences generated in step 1 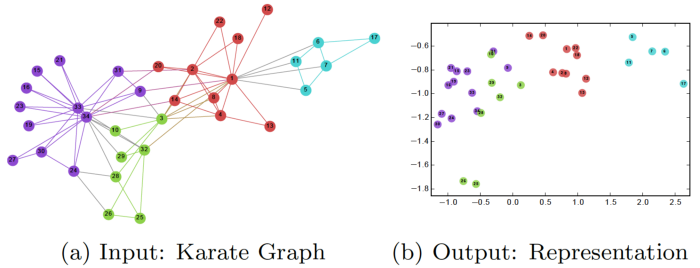Different colors indicate different labels
However, the main issue with DeepWalk is that it lacks the ability to generalize. Whenever a new node comes in, it has to re-train the model in order to represent this node (transductive). Thus, such GNN is not suitable for dynamic graphs where the nodes in the graphs are ever-changing.

The key idea is that the techniques which have been used to model natural language (where the symbol frequency follows a power law distribution (or Zipf ’s law)) can be repurposed to model community structure in networks. In this model, we generalizes the concept of language modeling to explore the graph through a stream of short random walks. These walks can be thought of short sentences and phrases in a special language. The direct analog is to estimate the likelihood of observing vertex $v_i$ given all the previous vertices visited so far in the random walk.

$P_r(v_i \vert (v_1,v_2,...,v_{i-1}))$

But since our goal is to learn a latent representation, not only a probability distribution of node co-occurrences, so we use a mapping function $Φ: v ∈ V \rightarrow \mathbb{R}^{|V|×d}$ . This mapping $Φ$ represents the latent social representation associated with each vertex v in the graph. The problem then, is to estimate the likelihood:

$ $Pr(v_i | (Φ(v_1), Φ(v_2), · · · , Φ(v_{i−1}))) $$

Although as the walk length grows, computing this objective function becomes un-feasible, skip-gram concept in language modeling can be employed to solve this problem. First, instead of using the context to predict a missing word, it uses one word to predict the context. Secondly, the context is composed of the words appearing to right side of the given word as well as the left side. Finally, it removes the ordering constraint on the problem. Instead, the model is required to maximize the probability of any word appearing in the context without the knowledge of its offset from the given word.

Below picture explains the process clearly:

What does it look like in code?

# Instantiate a undirected Networkx graph
G = nx.Graph()
G.add_edges_from(list_of_product_copurchase_edges)

def get_random_walk(graph:nx.Graph, node:int, n_steps:int = 4)->List[str]:
   """ Given a graph and a node, 
       return a random walk starting from the node 
   """
   local_path = [str(node),]
   target_node = node
   for _ in range(n_steps):
      neighbors = list(nx.all_neighbors(graph, target_node))
      target_node = random.choice(neighbors)
      local_path.append(str(target_node))
   return local_path

walk_paths = []

for node in G.nodes():
   for _ in range(10):
      walk_paths.append(get_random_walk(G, node))
 
walk_paths[0]
>>> [‘10001’, ‘10205’, ‘11845’, ‘10205’, ‘10059’]

What these random walks provide to us is a series of strings that act as a path from the start node — randomly walking from one node to the next down the list. What we do next is we treat this list of strings as a sentence, then utilize these series of strings to train a Word2Vec model:

# Instantiate word2vec model
embedder = Word2Vec(
   window=4, sg=1, hs=0, negative=10, alpha=0.03, min_alpha=0.0001,    
   seed=42
)

# Build Vocabulary
embedder.build_vocab(walk_paths, progress_per=2)

# Train
embedder.train(
   walk_paths, total_examples=embedder.corpus_count, epochs=20, 
   report_delay=1
)

It’s a slight stretch, but here’s the gist of it from the recommendations perspective:

Use the product pairs and associated relationships to create a graph
Generate sequences from the graph (via random walk)
Learn product embeddings based on the sequences (via word2vec)
Recommend products based on embedding similarity (e.g., cosine similarity, dot product)

DeepWalk

The DeepWalk process operates in a few steps​

Let's see how it works in depth​

What does it look like in code?​

Links​

The DeepWalk process operates in a few steps

Let's see how it works in depth

What does it look like in code?

Links