Markov Decision Process¶

The Markov decision process (MDP), a reinforcement learning (RL) algorithm, perfectly illustrates how machines have become intelligent in their own unique way. Humans build their decision process on experience. MDPs are memoryless. Humans use logic and reasoning to think problems through. MDPs apply random decisions 100% of the time. Humans think in words, labeling everything they perceive. MDPs have an unsupervised approach that uses no labels or training data. MDPs boost the machine thought process of self-driving cars (SDCs), translation tools, scheduling software, and more. This memoryless, random, and unlabeled machine thought process marks a historical change in the way a former human problem was solved.

MDP provides a mathematical framework for solving the RL problem. Almost all RL problems can be modeled as an MDP. MDPs are widely used for solving various optimization problems.

More formally, the RL problem is typically formulated as a Markov decision process (MDP) in the form of a tuple (S, A, R,P, γ), where S is the set of all possible states, A is the set of available actions in all states, R is the reward function, P is the transition probability, and γ is the discount factor. The goal of the RL agent is to find a policy π(a|s) that takes action a ∈ A in state s ∈ S in order to maximize the expected, discounted cumulative reward \(\max \mathbb{E}[R(\tau)]\) where \(R(\tau) = \sum_{t=0}^\tau \gamma^tr(a_t,s_t)\), 0≤ \(\gamma\) ≤ 1.

The objective of an agent in an MDP is to find an optimal policy \((π_θ : S × A \mapsto [0, 1])\) which maximizes the expected cumulative rewards from any state \(s ∈ S\), i.e., \(V^∗ (s) = max_{π_θ} \mathbb{E}_{π_θ}\{ \sum_{k=0}^\infty \gamma^k r{t+k}|s_t = s\}\), or maximizes equivalently the expected cumulative rewards from any state-action pair \(s ∈ S\), \(a ∈ A\), i.e., \(Q^∗ (s,a) = max_{π_θ} \mathbb{E}_{π_θ}\{ \sum_{k=0}^\infty \gamma^k r{t+k}|s_t = s, a_t=a\}\). Here \(\mathbb{E}_{π_θ}\) is the expectation under policy \(π_θ\), \(t\) is the current timestep and \(r_{t+k}\) is the immediate reward at a future timestep \(t + k\).

Recommender-User interactions in MDP¶

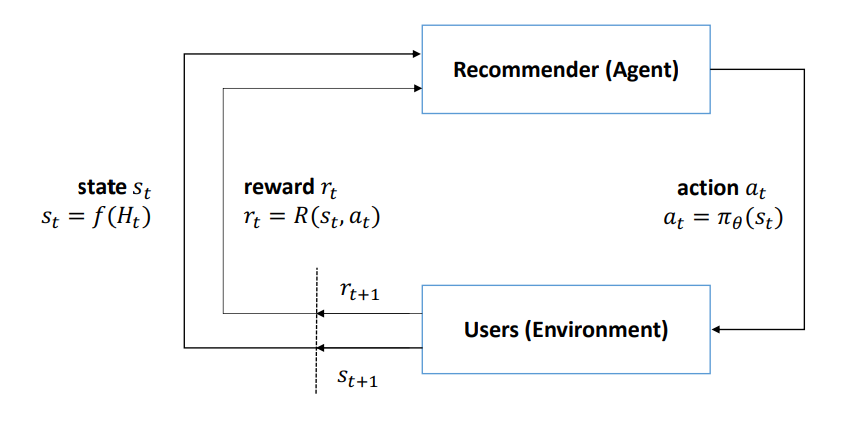
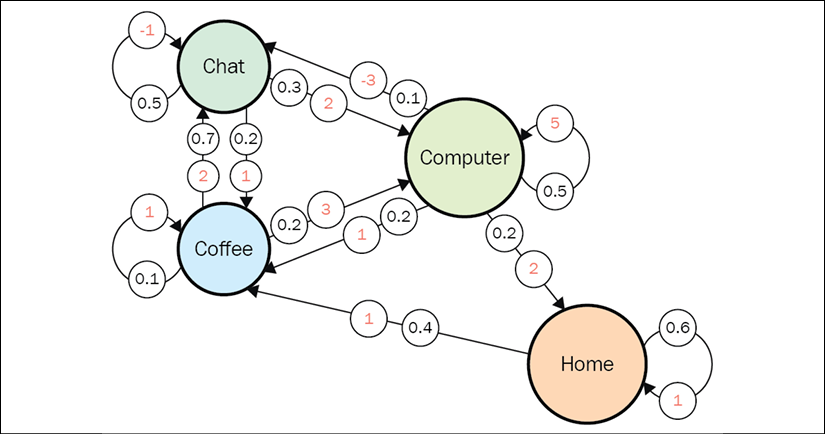
The above figure illustrates the recommender-user interactions in MDP formulation. Considering the current user state and immediate reward to the previous action, the recommender takes an action. Note that in our model, an action corresponds to neither recommending an item nor recommending a list of items. Instead, an action is a continuous parameter vector. Taking such an action, the parameter vector is used to determine the ranking scores of all the candidate items, by performing inner product with item embeddings. All the candidate items are ranked according to the computed scores and Top-N items are recommended to the user. Taking the recommendation from the recommender, the user provides her feedback to the recommender and the user state is updated accordingly. The recommender receives rewards according to the user’s feedback. Without loss of generalization, a recommendation procedure is a \(T\) timestep trajectory as \((s_0, a_0, r_0, s_1, a_1, r_1, ..., s_{T−1}, a_{T−1}, r_{T−1}, s_T )\).

The Markov property and Markov chain¶

The Markov property states that the future depends only on the present and not on the past. The Markov chain, also known as the Markov process, consists of a sequence of states that strictly obey the Markov property; that is, the Markov chain is the probabilistic model that solely depends on the current state to predict the next state and not the previous states, that is, the future is conditionally independent of the past.

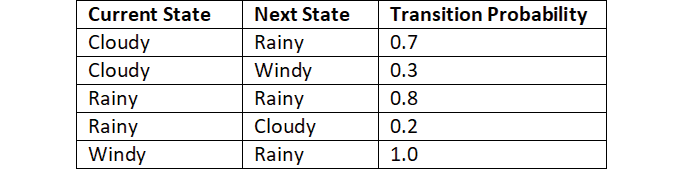
For example, if we want to predict the weather and we know that the current state is cloudy, we can predict that the next state could be rainy. We concluded that the next state is likely to be rainy only by considering the current state (cloudy) and not the previous states, which might have been sunny, windy, and so on.

However, the Markov property does not hold for all processes. For instance, throwing a dice (the next state) has no dependency on the previous number that showed up on the dice (the current state).

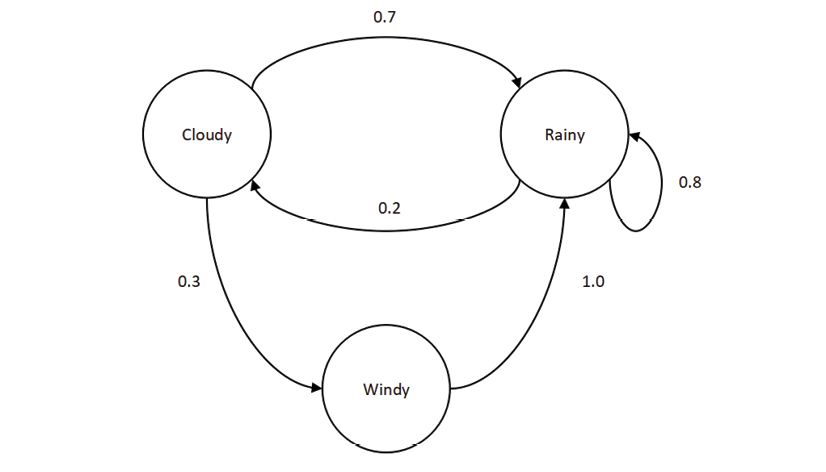
Moving from one state to another is called a transition, and its probability is called a transition probability. We denote the transition probability by \(P(s'|s)\). It indicates the probability of moving from the state \(*s\)* to the next state \(s'\). Say we have three states (cloudy, rainy, and windy) in our Markov chain. Then we can represent the probability of transitioning from one state to another using a table called a Markov table, as shown below:

We can also represent this transition information of the Markov chain in the form of a state diagram:

We can also formulate the transition probabilities into a matrix called the transition matrix:

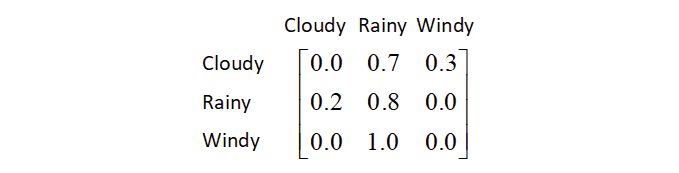
Thus, to conclude, we can say that the Markov chain or Markov process consists of a set of states along with their transition probabilities.

The Markov Reward Process¶

The Markov Reward Process (MRP) is an extension of the Markov chain with the reward function. That is, we learned that the Markov chain consists of states and a transition probability. The MRP consists of states, a transition probability, and also a reward function.

A reward function tells us the reward we obtain in each state. For instance, based on our previous weather example, the reward function tells us the reward we obtain in the state cloudy, the reward we obtain in the state windy, and so on. The reward function is usually denoted by \(*R(s)*\).

Thus, the MRP consists of states \(*s*\), a transition probability \(P(s'|s)\), and a reward function \(R(s)\).

The Markov Decision Process¶

The Markov Decision Process (MDP) is an extension of the MRP with actions. That is, we learned that the MRP consists of states, a transition probability, and a reward function. The MDP consists of states, a transition probability, a reward function, and also actions. We learned that the Markov property states that the next state is dependent only on the current state and is not based on the previous state. Is the Markov property applicable to the RL setting? Yes! In the RL environment, the agent makes decisions only based on the current state and not based on the past states. So, we can model an RL environment as an MDP.

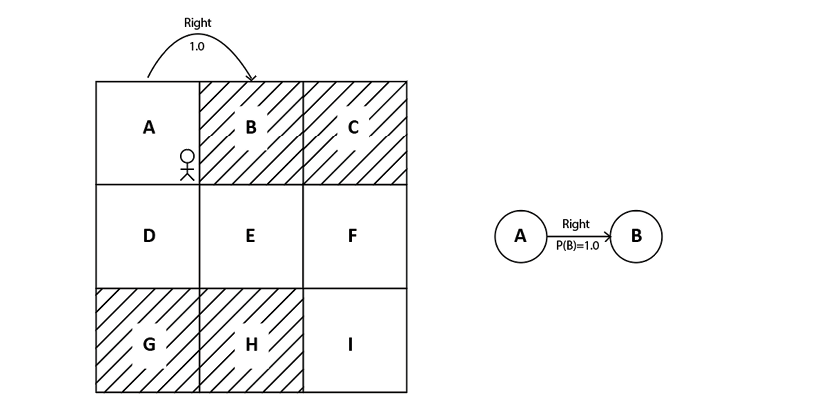
Let’s understand this with an example. Given any environment, we can formulate the environment using an MDP. For instance, let’s consider the same grid world environment, and the goal of the agent is to reach state I from state A without visiting the shaded states:

An agent makes a decision (action) in the environment only based on the current state the agent is in and not based on the past state. So, we can formulate our environment as an MDP. We learned that the MDP consists of states, actions, transition probabilities, and a reward function. Now, let’s learn how this relates to our RL environment:

States – A set of states present in the environment. Thus, in the grid world environment, we have states A to I.

Actions – A set of actions that our agent can perform in each state. An agent performs an action and moves from one state to another. Thus, in the grid world environment, the set of actions is up, down, left, and right.

Transition probability

– The transition probability is denoted by P(s’|s). It implies the probability of moving from a state \(*s\)* to the next state \(s'\). while performing an action a. If you observe, in the MRP, the transition probability is just \(P(s'|s)\), that is, the probability of going from state \(*s\)* to state \(s'\), and it doesn’t include actions. But in the MDP, we include the actions, and thus the transition probability is denoted by \(P(s'|s,a)\).

For example, in our grid world environment, say the transition probability of moving from state A to state B while performing an action right is 100%. This can be expressed as \(*P(B|A, right) = 1.0*\).

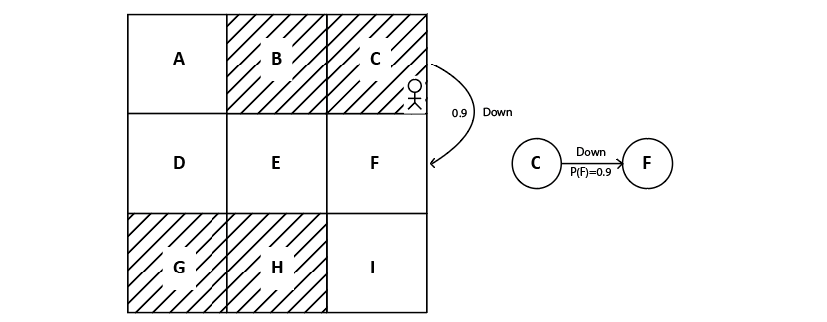
Suppose our agent is in state C and the transition probability of moving from state C to state F while performing the action down is 90%, then it can be expressed as \(P(F|C, down) = 0.9\). We can also view this in the state diagram:

The reward function is denoted by \(R(s,a,s')\). It represents the reward our agent obtains while transitioning from state s to state s’ while performing an action a.

Say the reward we obtain while transitioning from state A to state B while performing the action right is -1, then it can be expressed as R(A, right, B) = -1. We can also view this in the state diagram, as shown below:

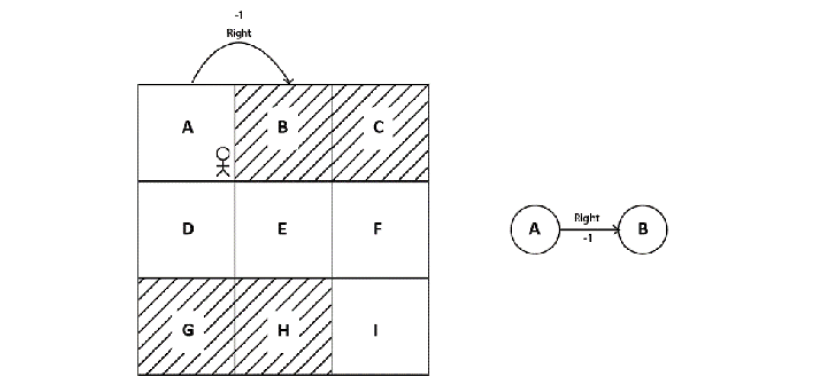
Thus, an RL environment can be represented as an MDP with states, actions, transition probability, and the reward function. But wait! What is the use of representing the RL environment using the MDP? We can solve the RL problem easily once we model our environment as the MDP. For instance, once we model our grid world environment using the MDP, then we can easily find how to reach the goal state I from state A without visiting the shaded states.