Counterfactual policy evaluation¶

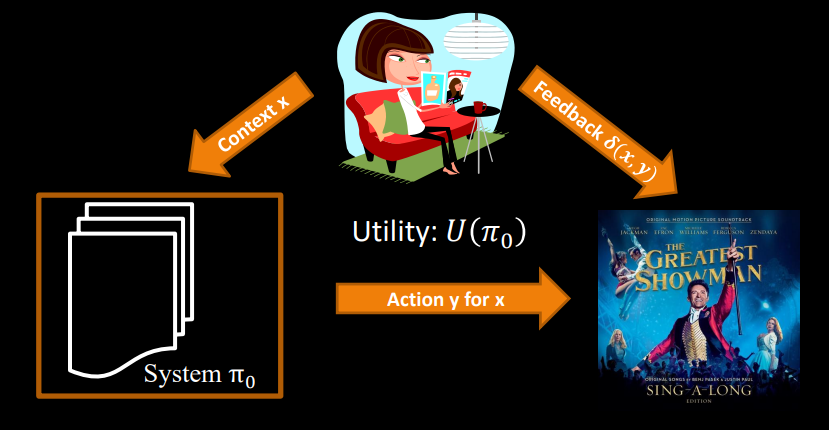
General Formulation: Contextual Bandits¶

Observes context vector \(x\) (e.g., user info)
Policy π selects an action \(y\) (e.g., recommend specific item)
Observes reward/feedback \(\delta(x,y)\) (e.g., click indicator)

Music voice assistant

Context \(x\): User and speech

Action \(y\): Track that is played

Feedback \(\delta(x,y)\): Listened to the end

Netflix banner

Context \(x\): User profile, time of day, day of week

Action \(y\): Movie to put in banner

Feedback \(\delta(x,y)\): Click, complete views, etc.

YouTube recommendations

Context \(x\): Current video, user demographics, past interactions

Action \(y\): Ranking of recommended videos

Feedback \(\delta(x,y)\): Click, downstream dwell time, etc.

News recommender

Context \(x\): User

Action \(y\): Portfolio of news articles

Feedback \(\delta(x,y)\): Reading time in minutes

Hiring

Context \(x\): Set of candidates, job description

Action \(y\): Person that is hired

Feedback \(\delta(x,y)\): Job performance of \(y\)

Medical

Context \(x\): Diagnostics

Action \(y\): BP/Stent/Drugs

Feedback \(\delta(x,y)\): Survival

Search engine

Context \(x\): Query

Action \(y\): Ranking

Feedback \(\delta(x,y)\): Clicks on SERP

Ad placement

Context \(x\): User, page

Action \(y\): Placed Ad

Feedback \(\delta(x,y)\): Click/No click

Online retail

Context \(x\): Category

Action \(y\): Tile layout

Feedback \(\delta(x,y)\): Purchases

Streaming media

Context \(x\): User

Action \(y\): Carousel layout

Feedback \(\delta(x,y)\): Plays

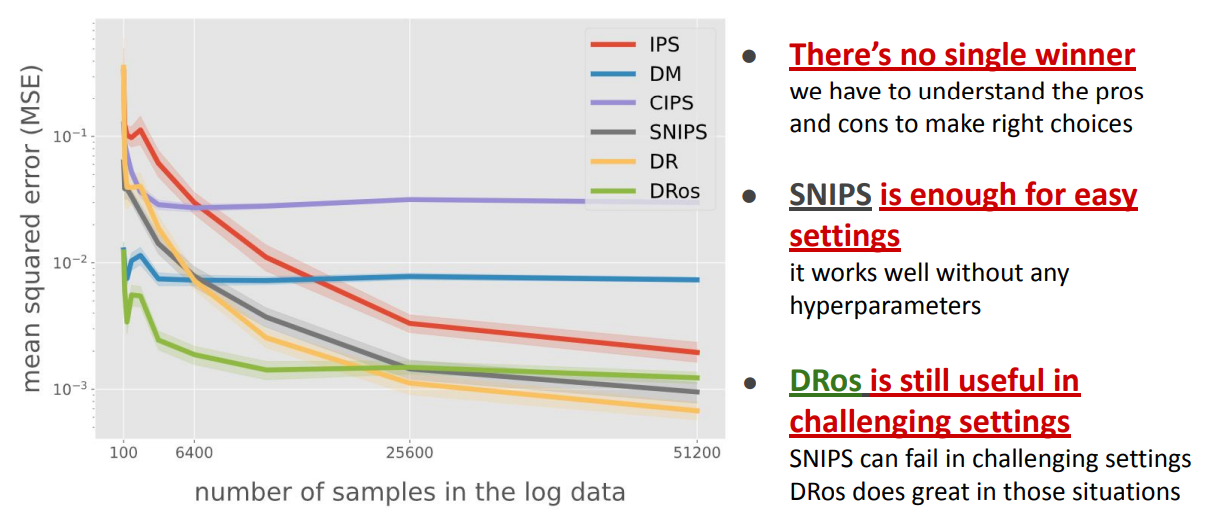
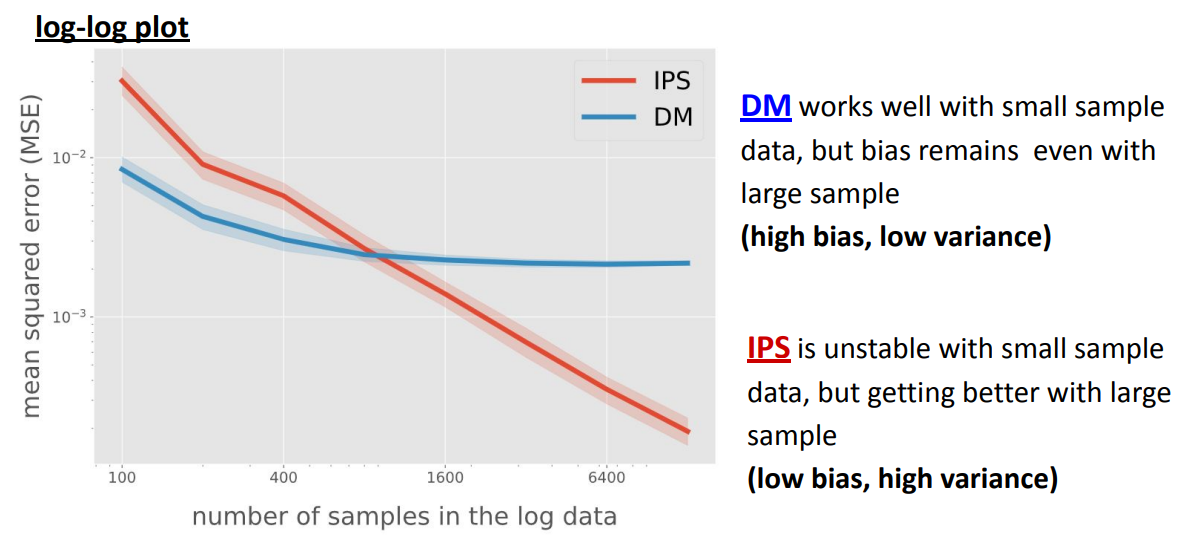
DM vs IPS: Bias-Variance Trade-off¶

CIPS and SNIPS - techniques to contain the IPS large weights¶

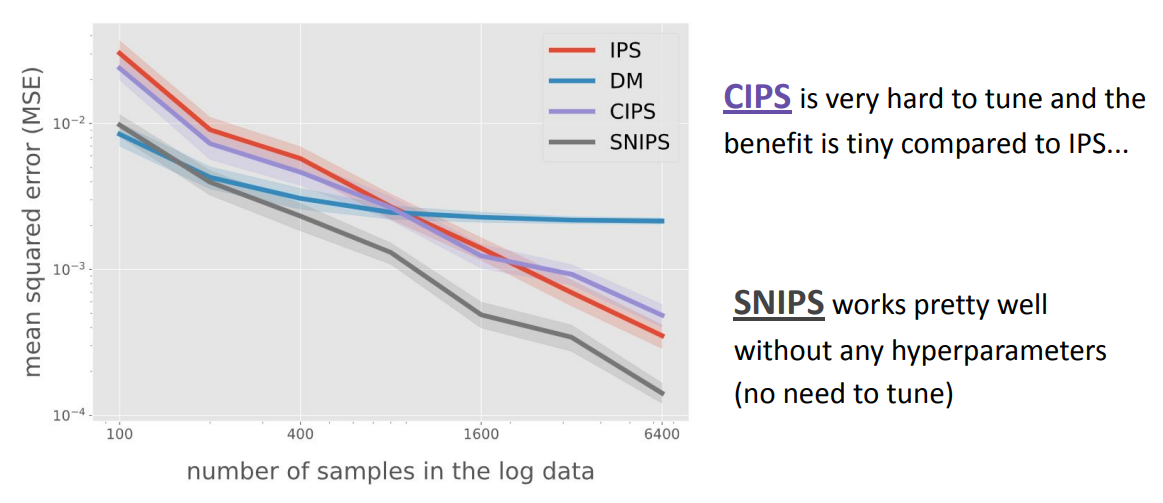
DM vs IPS vs CIPS vs SNIPS (varying sample size).

Summary of OPE Estimators¶

Combinatorial Action¶

In practice, the action space is often combinatorial, and a policy has to choose a set of (discrete) actions at the same time:

We have to modify the formulation a little bit, to adjust to the combinatorial setting:

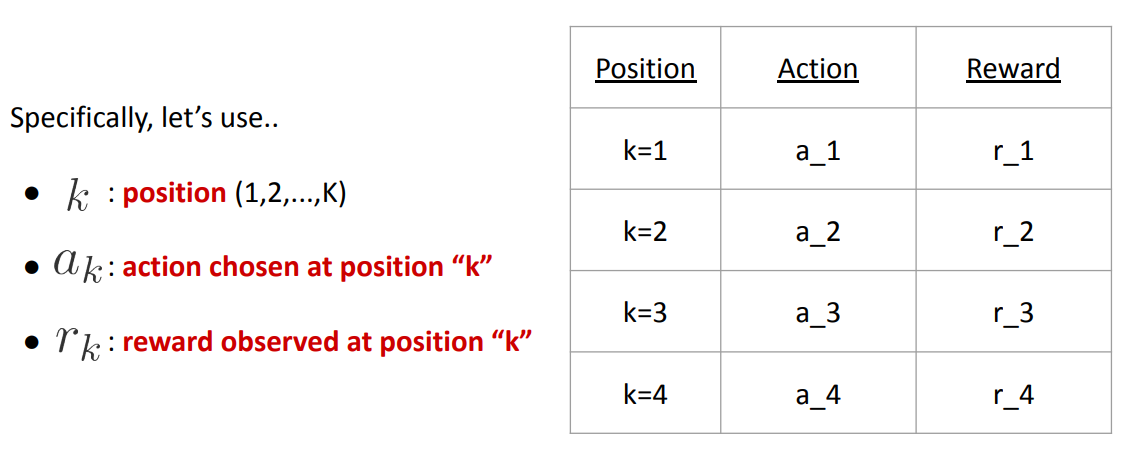
Even in the combinatorial action setting, we can (naively) use the IPS estimator to get unbiased/consistent estimate:

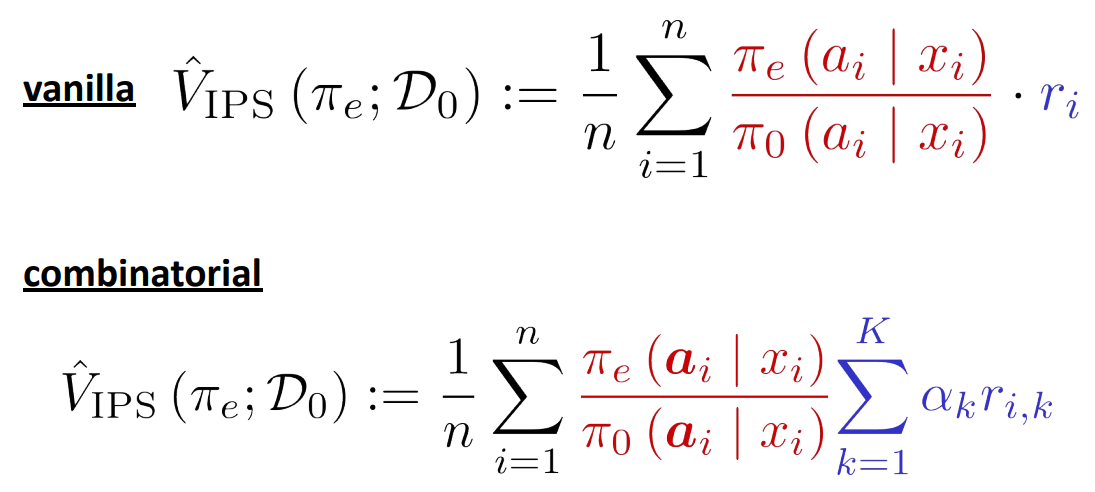
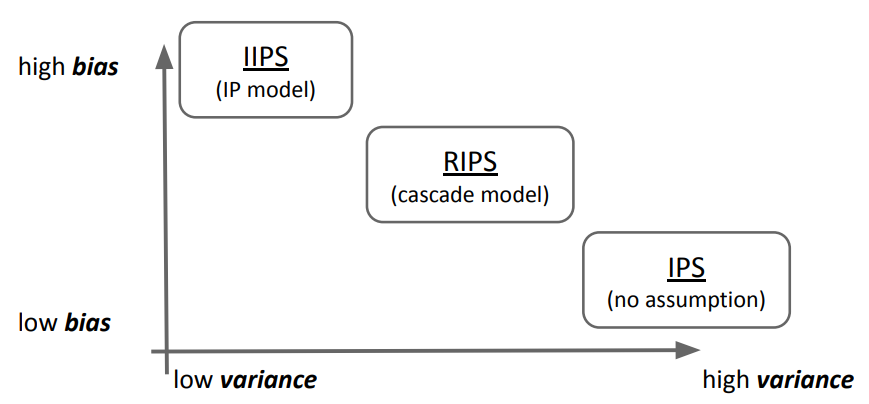
IPS, IIPS and RIPS¶

How to compare OPE/OPL methods in Experiments?¶

In OPL experiments, you as a researcher try to propose a policy learning method that can lead to a better policy value than existing methods.

OPL performance measure:

\[V(\pi_\phi) \coloneqq \mathop{\mathbb{E}}_{p(x)\pi_\phi(a \vert x)p(r \vert x,a)}[r]\]

We have to evaluate the policy value of the proposed and baseline policies and compare.

In OPE experiments, you as a researcher try to propose a OPE estimator that can lead to an accurate MSE (lower MSE) than existing estimators.

OPE performance measure:

\[MSE(\hat{V};\pi_e) \coloneqq \mathop{\mathbb{E}}_\mathcal{D_0}[(V(\pi_e)-\hat{V}(\pi_e;\mathcal{D}_0,\theta))^2]\]

We have to evaluate the MSE of the proposed and baseline estimators and compare.