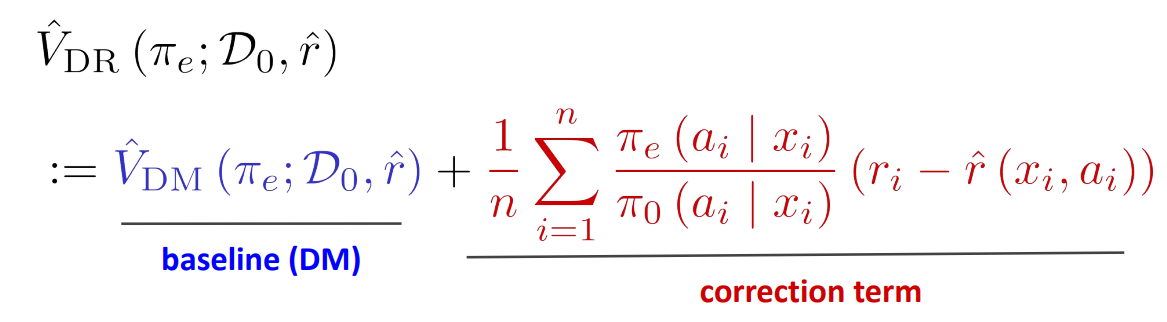Doubly Robust¶
The doubly robust technique combines the direct method with inverse propensity scores. An intuitive way to think about it is to consider that it uses the predicted rewards from the direct method, and if there is additional information (i.e. exploration and target policy actions match) then the inverse propensity score correction is applied. This is illustrated below.
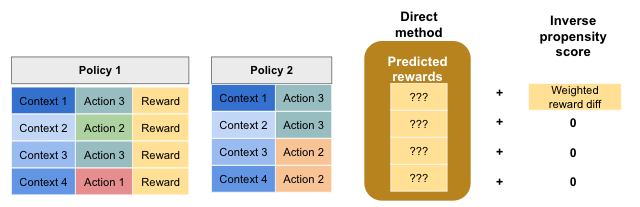
This technique is doubly robust, because if either the direct method or the inverse propensity score component is accurate, then the final reward estimate is accurate.
This method is interesting in that it combines IPS and the DM in a clever and beneficial way. As said in the DR paper,
Doubly robust estimators take advantage of both the estimate of the expected reward rand the estimate of action probabilities \({\hat{\mu}_{k}(a\vert x)}\)… If either one of the two estimators (i.e., DM or IPS) is correct, then the estimation is unbiased. This method thus increases the chances of drawing reliable inference.
As demonstrated in the paper, this method is a strict improvement over both the direct method and IPS.
Formally, the DR estimate is defined as follows:
where, \(\hat{r}(x_k,\nu) = \sum_{\alpha \in \mathcal{A}}{\nu(a\vert x_k)}\hat{r}(x_k,a)\), and,
\(\hat{V}_{DR}\) = the expected average reward per decision under the new policy
\(n\) = the number of samples in your historical data
\({\nu(a_k\vert x_k)}\) = the probability that your new policy takes the logged action given the logged context
\({\hat{\mu}_{k}(a_k\vert x_k)}\) = the probability that your logging policy takes the logged action given the logged context
\(r_k\) = the logged reward from taking that action given that context
\(\hat{r}(x_k,a_k)\) = the predicted reward given a context and action
In the formula above you can see that the doubly robust method takes the direct method and applies a correction based on the action distribution mismatch and reward model prediction error. If the reward model prediction error is 0 on a specific sample, then the entire second term cancels out and you are simply left with the direct method. As the doubly robust paper puts it, “…the doubly robust estimator uses [the reward model] as a baseline and if there is data available, a correction is applied”.